题目内容
如图，设D是图中边长分别为2和4的矩形区域，E是D内位于函数y=x2图象下方的区域（阴影部分），向D内随机抛掷30个点，则落在E内的点的个数约为（ ）| A、15 | B、20 | C、5 | D、10 |
分析：欲求落在E内的点的个数，则可建立关于x，y的直角坐标系，画出关于x和y的平面区域，再根据几何概型概率公式结合定积分求面积的方法易求解．
解答：解：本题是几何概型问题，
区域E的面积为：
S1=
x2dx=
x3
=
，
∴“该点在E中的概率”事件对应的区域面积为
，
则落在E内的点的概率是
=
．
设落在E内的点的个数为n，∴
=
，n=10
故选D．
区域E的面积为：
S1=
| ∫ | 2 0 |
| 1 |
| 3 |
| | | 2 0 |
| 8 |
| 3 |
∴“该点在E中的概率”事件对应的区域面积为
| 8 |
| 3 |
则落在E内的点的概率是
| ||
| 8 |
| 1 |
| 3 |
设落在E内的点的个数为n，∴
| n |
| 30 |
| 1 |
| 3 |
故选D．
点评：本题综合考查了二次函数的图象，几何概型，及定积分在求面积中的应用，考查计算能力与转化思想．属于基础题．
练习册系列答案
相关题目
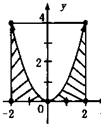如图，设D是图中边长为4的正方形区域，E是D内函数y=x2图象下方的点构成的区域．在D内随机取一点，则该点在E中的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
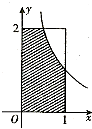如图，设D是图中边长分别为1和2的矩形区域，E是D内位于函数
（2012•道里区三模）如图，设D是图中边长分别为1和2的矩形区域，E是D内位于函数y=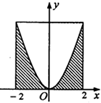
如图，设D是图中边长为4的正方形区域，E是D内函数y=x2图象下方的点构成的区域．向D中随机投一点，则该点落入E中的概率为