Question

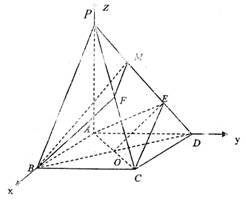
（08年青岛市质检一理）  （12分）如图，在底面是正方形的四棱锥P―ABCD中，PA=AC=2，PB=PD=，点E在PD上，且PE：ED=2：1。

   （I）在棱PC上是否存在一点F，使得BF//平面AEC？证明你的结论；

   （II）求二面角P―AC―E的平面角的大小。

 

Answer 1

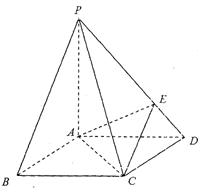
解析:证明：（I）当F是棱PC的中点，则有BF//平面AEC

    取PE中点M，连执着FM，BM，连接BD

    交AC于O，连接OE

    ∵F，M分别是PC，PE的中点

∴FM∥CE，

又FM面AEC，CE面AEC

∴FM∥面AEC …………3分

又E是DM的中点

OE//BM，OE平面AEC，BM面AEC

∴BM∥面AEC且BM∩FM=M

∴平面BFM∥平面ACE

又BF平面BFM

∴BF∥平面ACE …………6分

   （II）在底面是正方形的四棱锥P―ABCD中，PA=AC=2，PB=PD=，

∴AB=AD=

∴PB²=PA²+AB²，PD²=PA²+AD²

∴PA⊥AB，PA⊥AD

∴PA⊥面ABCD                                                                     …………7分

建立如图所示坐标系A―xyz

则有A（0，0，0），P（0，0，2），D（），O

面PAC

∴面PAC的法向量为                        …………9分

设面AEC的法向量，

由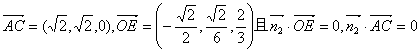得：

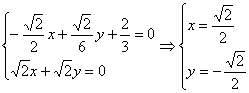                                …………10分

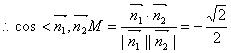
∴二面角P―AC―E的平面角的值为          …………12分