题目内容
18.已知ABCDEF是正六边形,且$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$,则$\overrightarrow{CD}$=$\frac{1}{2}$($\overrightarrow{b}$$-\overrightarrow{a}$).分析 画出图形,根据条件可得到$\overrightarrow{BE}=\overrightarrow{b}-\overrightarrow{a}$,而$CD=\frac{1}{2}BE$,从而便可得到$\overrightarrow{CD}=\frac{1}{2}(\overrightarrow{b}-\overrightarrow{a})$.
解答  解:如图,
解:如图,
连接EB,则:$\overrightarrow{BE}=\overrightarrow{AE}-\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}$;
$CD=\frac{1}{2}BE$;
∴$\overrightarrow{CD}=\frac{1}{2}\overrightarrow{BE}=\frac{1}{2}(\overrightarrow{b}-\overrightarrow{a})$.
故答案为:$\frac{1}{2}(\overrightarrow{b}-\overrightarrow{a})$.
点评 考查向量减法的几何意义,向量数乘的几何意义,共线向量基本定理,以及对正六边形的认识.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
8.欲寄出两封信,现有两个邮箱供选择,则两封信都投到一个邮箱的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{8}$ |
6.已知函数f(x)=ax2-ex,f′(-1)=-4,则函数y=f(x)的零点所在的区间是( )
| A. | (-3,-2) | B. | (-1,0) | C. | (0,1) | D. | (4,5) |
10.设函数f(x)=ex(2x-1)+ax-a,其中a>-1,若关于x不等式f(x)<0的整数解有且只有一个,则实数a的取值范围为( )
| A. | (-1,$\frac{3}{2e}$] | B. | (-$\frac{3}{4}$,$\frac{3}{2e}$] | C. | (-$\frac{3}{4}$,-$\frac{3}{2e}$] | D. | (-1,-$\frac{3}{2e}$] |
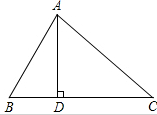 如图,在△ABC中,AD⊥BC,$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$,BD=4,CD=6.
如图,在△ABC中,AD⊥BC,$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$,BD=4,CD=6.