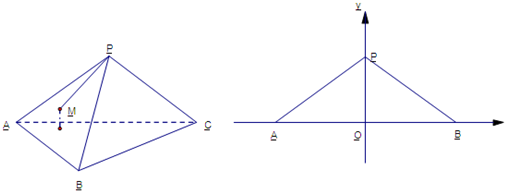
题目内容
已知正三棱锥P-ABC的体积为72
,侧面与底面所成的二面角的大小为60°.
(1)证明:PA⊥BC;
(2)求底面中心O到侧面的距离.
| 3 |
(1)证明:PA⊥BC;
(2)求底面中心O到侧面的距离.


(1)证明:取BC边的中点D,连接AD、PD,
则AD⊥BC,PD⊥BC,故BC⊥平面APD.∴PA⊥BC.
(2)如图,由(1)可知平面PBC⊥平面APD,
则∠PDA是侧面与底面所成二面角的平面角.
过点O作OE⊥PD,?E为垂足,则OE就是点O到侧面的距离.
设OE为h,由题意可知点O在AD上,
∴∠PDO=60°,OP=2h.
∵?OD=
| 2h | ||
|
∴S△ABC=
| ||
| 4 |
| 3 |
∵72
| 3 |
| 1 |
| 3 |
| 3 |
8
| ||
| 3 |
即底面中心O到侧面的距离为3.

练习册系列答案
相关题目
 已知正三棱锥P-ABC主视图如图所示,其中△PAB中,AB=PC=2cm,则这个正三棱锥的左视图的面积为
已知正三棱锥P-ABC主视图如图所示,其中△PAB中,AB=PC=2cm,则这个正三棱锥的左视图的面积为