题目内容
建立适当的坐标系，证明：等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高．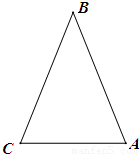
【答案】分析：建立平面直角坐标系，如图，求出AB的方程、BC的方程，在边CA上任取一点P（m，0），-a≤m≤a，求出P到AB的
距离PE，P到CB的距离为PF的值，再求出A到BC的距离为 h，可得PE+PF=h，命题得证．
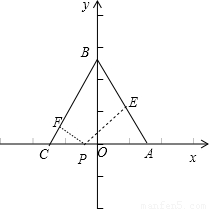
解答：证明：设等腰三角形为ABC，以CA所在的直线为x轴，以CA的垂直平分线为y轴，建立平面直角坐标系，如图：
设A（a，0）、C（-a，0）、B（0，b），a＞0，b＞0．
则AB的方程为bx+ay-ab=0，BC的方程为bx-ay+ab=0，在边CA上任取一点P（m，0），-a≤m≤a，
则P到AB的距离PE=
=
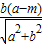，P到CB的距离为PF=
=
．
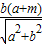故PE+PF=
=
．
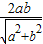而A到BC的距离为 h=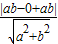
=
．
故PE+PF=h，即等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高．
点评：本题主要考查用坐标法明数学命题，用截距式求直线的方程，点到直线的距离公式的应用，属于中档题．
距离PE，P到CB的距离为PF的值，再求出A到BC的距离为 h，可得PE+PF=h，命题得证．
解答：证明：设等腰三角形为ABC，以CA所在的直线为x轴，以CA的垂直平分线为y轴，建立平面直角坐标系，如图：
设A（a，0）、C（-a，0）、B（0，b），a＞0，b＞0．
则AB的方程为bx+ay-ab=0，BC的方程为bx-ay+ab=0，在边CA上任取一点P（m，0），-a≤m≤a，
则P到AB的距离PE=
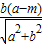=，P到CB的距离为PF==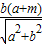．故PE+PF=
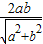=．而A到BC的距离为 h=
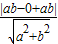=．故PE+PF=h，即等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高．
点评：本题主要考查用坐标法明数学命题，用截距式求直线的方程，点到直线的距离公式的应用，属于中档题．
练习册系列答案
金钥匙试卷系列答案
相关题目
建立适当的坐标系，证明：等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高．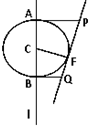
（2007•湛江二模）如图，F是定直线l外的一个定点，C是l上的动点，有下列结论：若以C为圆心，CF为半径的圆与l相交于A、B两点，过A、B分别作l的垂线与圆C过F的切线相交于点P和点Q，则必在以F为焦点，l为准线的同一条抛物线上．
