题目内容
建立适当的坐标系，证明：等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。
| 证明：如图，设△ABC是等腰三角形，以底边CA所在直线为x轴，以过顶点B且垂直于CA的直线为y轴，建立直角坐标系， 设A（a，0），B（0，b），（a>0， b>0）则C（-a，0）， 直线AB的方程为bx+ay-ab=0， 直线BC的方程bx-ay+ab=0， 设底边CA上任意一点P（x，0）（-a≤x≤a） 则点P到AB的距离  ，点P到BC的距离  ，点A到BC的距离  ，所以  ， 因此，等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高。 |
 |
练习册系列答案
应用题作业本系列答案
相关题目
建立适当的坐标系，证明：等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高．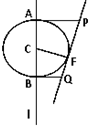
（2007•湛江二模）如图，F是定直线l外的一个定点，C是l上的动点，有下列结论：若以C为圆心，CF为半径的圆与l相交于A、B两点，过A、B分别作l的垂线与圆C过F的切线相交于点P和点Q，则必在以F为焦点，l为准线的同一条抛物线上．
