题目内容
已知函数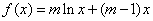
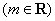 .
.
(Ⅰ)当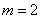 时,求曲线
时,求曲线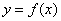 在点
在点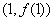 处的切线方程;
处的切线方程;
(Ⅱ)讨论 的单调性;
的单调性;
(III)若 存在最大值
存在最大值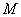 ,且
,且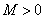 ,求
,求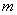 的取值范围.
的取值范围.
解:(Ⅰ)当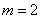 时,
时, .
.
 .
.
所以 .
.
又 ,
,
所以曲线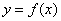 在点
在点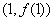 处的切线方程是
处的切线方程是 ,
,
即 .
.
(Ⅱ)函数 的定义域为
的定义域为 ,
,
 .
.
当 时,由
时,由 知
知 恒成立,
恒成立,
此时 在区间
在区间 上单调递减.
上单调递减.
当 时,由
时,由 知
知 恒成立,
恒成立,
此时 在区间
在区间 上单调递增.
上单调递增.
当 时,由
时,由 ,得
,得 ,由
,由 ,得
,得 ,
,
此时 在区间
在区间 内单调递增,在区间
内单调递增,在区间 内单调递减.
内单调递减.
(III)由(Ⅱ)知函数 的定义域为
的定义域为 ,
,
当 或
或 时,
时, 在区间
在区间 上单调,此时函数
上单调,此时函数 无最大值.
无最大值.
当 时,
时, 在区间
在区间 内单调递增,在区间
内单调递增,在区间 内单调递减,
内单调递减,
所以当 时函数
时函数 有最大值.
有最大值.
最大值 .
.
因为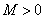 ,所以有
,所以有 ,解之得
,解之得 .
.
所以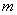 的取值范围是
的取值范围是 .
.

练习册系列答案
相关题目
对于函数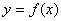 ,部分
,部分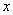 与
与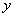 的对应关系如下表:
的对应关系如下表:
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
| 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
数列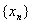 满足
满足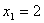 ,且对任意
,且对任意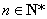 ,点
,点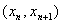 都在函数
都在函数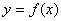 的图象上,则
的图象上,则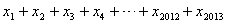 的值为
的值为
(A)9394 (B)9380 (C)9396 (D)9400
 列
列 的前
的前 项和为
项和为 ,若
,若 ,则公比为( )
,则公比为( ) 或
或 D.2或-2
D.2或-2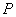 是棱长为1的正方体
是棱长为1的正方体 的底面
的底面 上一点,则
上一点,则 的取值范围是
的取值范围是 B.
B. C.
C. D.
D.
 ,抛物线
,抛物线 的焦点是
的焦点是 ,若抛物线上存在一点
,若抛物线上存在一点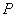 ,使得
,使得 最小,则
最小,则 (B)
(B) (C)
(C) (D)
(D)
 的图象为
的图象为 ,有如下结论:①图象
,有如下结论:①图象 对称;②图象
对称;②图象 对称;③函数
对称;③函数 内是增函数,其中正确的结论序号是 .(写出所有正确结论的序号)
内是增函数,其中正确的结论序号是 .(写出所有正确结论的序号) ”是“
”是“ ”的
”的 与点
与点 重合,
重合, 重合的点是
重合的点是 B.
B. C.
C. D.
D.
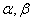 是非零实数,则“
是非零实数,则“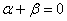 ”是“
”是“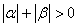 ”成立的( )
”成立的( ) 不充分条件
不充分条件