题目内容
正方体ABCD﹣A1B1C1D1的棱长为1,若动点P在线段BD1上运动,则![]() 的取值范围是 .
的取值范围是 .
考点:
平面向量数量积的运算.
专题:
平面向量及应用.
分析:
建立空间直角坐标系,求出有关点的坐标可得![]() 、
、![]() 、
、![]() 、
、![]() 的坐标,再由
的坐标,再由 ![]() =1﹣λ∈[0,1],可得
=1﹣λ∈[0,1],可得![]() 的取值范围.
的取值范围.
解答:
解:以![]() 所在的直线为x轴,以
所在的直线为x轴,以![]() 所在的直线为y轴,以
所在的直线为y轴,以![]() 所在的直线为z轴,建立空间直角坐标系.
所在的直线为z轴,建立空间直角坐标系.
则D(0,0,0)、C(0,1,0)、A(1,0,0)、B(1,1,0)、D1(0,0,1).
∴![]() =(0,1,0)、
=(0,1,0)、![]() (﹣1,﹣1,1).
(﹣1,﹣1,1).
∵点P在线段BD1上运动,∴![]() =λ•
=λ•![]() =(﹣λ,﹣λ,λ),且0≤λ≤1.
=(﹣λ,﹣λ,λ),且0≤λ≤1.
∴![]() =
=![]() +
+![]() =
=![]() +
+![]() =(﹣λ,1﹣λ,λ),
=(﹣λ,1﹣λ,λ),
∴![]() =1﹣λ∈[0,1],
=1﹣λ∈[0,1],
故答案为[0,1].
点评:
本题主要考查两个向量坐标形式的运算,两个向量的数量积公式,属于中档题.

练习册系列答案
相关题目
两球O1和O2在棱长为1的正方体ABCD-A1B1C1D1的内部,且互相外切,若球O1与过点A的正方体的三个面相切,球O2与过点C1的正方体的三个面相切,则球O1和O2的表面积之和的最小值为( )
A、(6-3
| ||
B、(8-4
| ||
C、(6+3
| ||
D、(8+4
|
在正方体ABCD-A1B1C1D1中,异面直线BC1与AB1所成角的大小为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,正方体ABCD-A1B1C1D1的棱长为6,动点M在棱A1B1上.
如图,正方体ABCD-A1B1C1D1的棱长为6,动点M在棱A1B1上.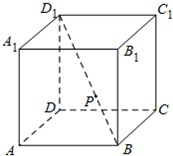 (2013•北京)如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )
(2013•北京)如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )