题目内容
设x>0,x≠1,求证:(1+xn)(1+x)n>2n+1xn(n∈N).
证明:(1)n=1时,左边=(1+x)2,右边=4x,
∵(1+x)2-4x=(1-x)2>0,
∴(1+x)2>4x.∴n=1时命题正确.
(2)假设n=k(k∈N且k≥1)时命题正确,即(1+xk)(1+x)k>2k+1xk,则n=k+1时,(1+xk+1)(1+x)k+1-2k+2xk+1=(1+xk+1)(1+x)k+1-2x·2k+1xk>(1+xk+1)(1+x)k+1-2x(1+xk)(1+x)k
=(1+x)k[(1+x)(1+xk+1)-2x(1+xk)]
=(1+x)k(1+x+xk+1+xk+2-2x-2xk+1)
=(1+x)k(1-x)(1-xk+1),
∵x>0且x≠1,
∴1-x与1-xk+1同号.
∴(1+x)k·(1-x)(1-xk+1)>0.
∴(1+xk+1)(1+x)k+1>2(k+1)+1xk+1.
∴n=k+1时命题正确.

练习册系列答案
相关题目
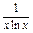 (x>0且x≠1).
(x>0且x≠1).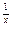 >xa对任意x∈(0,1)成立,求实数a的取值范围.
>xa对任意x∈(0,1)成立,求实数a的取值范围. (x>0且x≠1).
(x>0且x≠1). >xa对任意x∈(0,1)成立,求实数a的取值范围.
>xa对任意x∈(0,1)成立,求实数a的取值范围.