题目内容
设曲线y=cosx与x轴、y轴、直线 围成的封闭图形的面积为b,若g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,则实数k的取值范围是________.
围成的封闭图形的面积为b,若g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,则实数k的取值范围是________.
[0,+∞)
分析:由曲线y=cosx与x轴、y轴、直线 围成的封闭图形的面积为b,b为函数y=cosx在[0,
围成的封闭图形的面积为b,b为函数y=cosx在[0, ]上的定积分,求出b后代入函数g(x)=2lnx-2bx2-kx,由g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,可知其导函数在[1,+∞)上小于等于0恒成立,然后利用分离变量法可求k的取值范围.
]上的定积分,求出b后代入函数g(x)=2lnx-2bx2-kx,由g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,可知其导函数在[1,+∞)上小于等于0恒成立,然后利用分离变量法可求k的取值范围.
解答:由题意可知,b=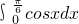 =
= =sin
=sin -sin0=
-sin0= -0=
-0= .
.
则g(x)=2lnx-2bx2-kx=2lnx-x2-kx.
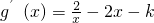 ,
,
由g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,
则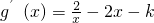 ≤0在[1,+∞)上恒成立,
≤0在[1,+∞)上恒成立,
即k≥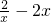 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
令t(x)=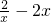 ,
,
则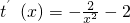 .
.
当x∈[1,+∞)时,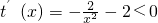
所以,函数t(x)=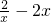 在[1,+∞)上为减函数,
在[1,+∞)上为减函数,
则t(x)max=t(1)=0,
所以,k≥0.
所以,使g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减的实数k的取值范围是[0,+∞).
故答案为[0,+∞).
点评:本题考查了定积分的求法,考查了利用函数得到函数研究函数的单调性,训练了利用分离变量求参数的取值范围,此题属中档题.
分析:由曲线y=cosx与x轴、y轴、直线
 围成的封闭图形的面积为b,b为函数y=cosx在[0,
围成的封闭图形的面积为b,b为函数y=cosx在[0, ]上的定积分,求出b后代入函数g(x)=2lnx-2bx2-kx,由g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,可知其导函数在[1,+∞)上小于等于0恒成立,然后利用分离变量法可求k的取值范围.
]上的定积分,求出b后代入函数g(x)=2lnx-2bx2-kx,由g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,可知其导函数在[1,+∞)上小于等于0恒成立,然后利用分离变量法可求k的取值范围.解答:由题意可知,b=
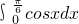 =
= =sin
=sin -sin0=
-sin0= -0=
-0= .
.则g(x)=2lnx-2bx2-kx=2lnx-x2-kx.
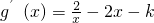 ,
,由g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,
则
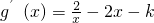 ≤0在[1,+∞)上恒成立,
≤0在[1,+∞)上恒成立,即k≥
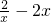 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,令t(x)=
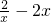 ,
,则
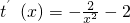 .
.当x∈[1,+∞)时,
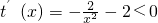
所以,函数t(x)=
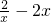 在[1,+∞)上为减函数,
在[1,+∞)上为减函数,则t(x)max=t(1)=0,
所以,k≥0.
所以,使g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减的实数k的取值范围是[0,+∞).
故答案为[0,+∞).
点评:本题考查了定积分的求法,考查了利用函数得到函数研究函数的单调性,训练了利用分离变量求参数的取值范围,此题属中档题.

练习册系列答案
相关题目
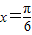 围成的封闭图形的面积为b,若g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,则实数k的取值范围是 .
围成的封闭图形的面积为b,若g(x)=2lnx-2bx2-kx在[1,+∞)上单调递减,则实数k的取值范围是 .