题目内容
在
中，内角
，
，
的对边分别为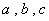
.已知
，
，且
.
(1)求
的值；(2)求边
的长．
[规范解答] (1)∵A，B，C为△ABC的内角，且A＝
，cos B＝
，
∴C＝π－(A＋B)，sin B＝
，
∴sin C＝sin(A＋B)＝sin Acos B＋cos Asin B＝
.
(2)由余弦定理得：
c2＝a2＋(
－1)b＝b2＋c2－2bccos A＋(－1)b，即b－c＋－1＝0.
又由正弦定理得c＝
＝
b，则b＝2.所以边b的长为2.
[规范解答] (1)∵A，B，C为△ABC的内角，
且A＝，cos B＝，
∴C＝π－(A＋B)，sin B＝，
∴sin C＝sin(A＋B)＝sin Acos B＋cos Asin B＝.
(2)由余弦定理得：
c2＝a2＋(－1)b＝b2＋c2－2bccos A＋(－1)b，即b－c＋－1＝0.
又由正弦定理得c＝＝b，则b＝2.所以边b的长为2.
练习册系列答案
新课标同步训练系列答案
相关题目
”是“一元二次方程
有实数解的” 条件 (必要不充分或充分不必要或充要或既不充分也不必要)
, 且n∈N*）, 则数列{ an} 的通项公式为 （ ）
B．
C．an=n+2 D．an=（ n+2）·3 n
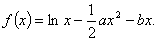
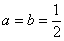时，求函数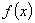
的单调区间；
＜
≤
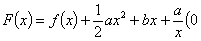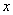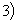，其图像上任意一点P
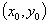处切线的斜率
≤
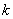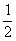恒成立，求实数
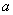的取值范围；
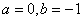时，方程
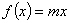在区间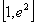
内有唯一实数解，求实数
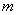的取值范围。
.
，求
的值；
的最大值和单调递增区间．
若M=
把直线l：2x+y+7=0变换为自身，则
，
．
R3 B. 
πR3 C. 
R3 D. 
R3
、
满足
，且
，则
B．
C．
D．