题目内容
已知函数 ,且对任意的x、y∈(-1,1)都有
,且对任意的x、y∈(-1,1)都有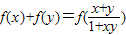 .
.(1)若数列
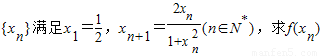 .
.(2)求
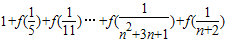 的值.
的值.
【答案】分析:(1)由题意得 ,从而∴{f(xn)}是以-1为首项,以2为公比的等比数列,故可求;(2)先证f(x)在(-1,1)上为奇函数,再用裂项求和法求和.
,从而∴{f(xn)}是以-1为首项,以2为公比的等比数列,故可求;(2)先证f(x)在(-1,1)上为奇函数,再用裂项求和法求和.
解答:解:(1)∵ .∴
.∴ …(3分)
…(3分) 
而 .…(5分)∴
.…(5分)∴ ∴{f(xn)}是以-1为首项,以2为公比的等比数列,故f(xn)=-2n-1…(7分)
∴{f(xn)}是以-1为首项,以2为公比的等比数列,故f(xn)=-2n-1…(7分)
(2)由题设,有 …(8分)
…(8分)
又 ,
,
得f(-x)=-f(x),故知f(x)在(-1,1)上为奇函数…(10分) 由 =
=
得 ,
,
于是
故 .…(12分)
.…(12分)
点评:本题主要考查等比数列的定义及裂项求和法求和,考查学生分析解决问题的能力,属于难题
 ,从而∴{f(xn)}是以-1为首项,以2为公比的等比数列,故可求;(2)先证f(x)在(-1,1)上为奇函数,再用裂项求和法求和.
,从而∴{f(xn)}是以-1为首项,以2为公比的等比数列,故可求;(2)先证f(x)在(-1,1)上为奇函数,再用裂项求和法求和.解答:解:(1)∵
 .∴
.∴ …(3分)
…(3分) 
而
 .…(5分)∴
.…(5分)∴ ∴{f(xn)}是以-1为首项,以2为公比的等比数列,故f(xn)=-2n-1…(7分)
∴{f(xn)}是以-1为首项,以2为公比的等比数列,故f(xn)=-2n-1…(7分)(2)由题设,有
 …(8分)
…(8分)又
 ,
,得f(-x)=-f(x),故知f(x)在(-1,1)上为奇函数…(10分) 由
 =
=
得
 ,
,于是

故
 .…(12分)
.…(12分)点评:本题主要考查等比数列的定义及裂项求和法求和,考查学生分析解决问题的能力,属于难题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,且对任意
,且对任意 ,有
,有 .
. ;
; 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数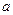 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
)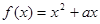 ,且对任意的实数
,且对任意的实数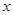 都有
都有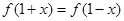 成立.
成立.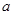 的值;
的值;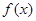 在区间
在区间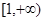 上是增函数.
上是增函数.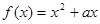 ,且对任意的实数x都有
,且对任意的实数x都有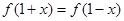 成立,求实数a的值;
成立,求实数a的值; 是减函数,且
是减函数,且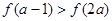 ,求a的取值范围。
,求a的取值范围。 ,且对任意的x、y∈(-1,1)都有
,且对任意的x、y∈(-1,1)都有 .
. .
.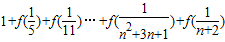 的值.
的值.