题目内容
已知函数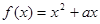
，且对任意的实数
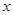都有
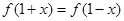成立.
（1）求实数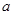
的值；
（2）利用函数单调性的定义证明函数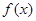
在区间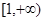
上是增函数.
【答案】
（1）
（2）严格按照单调性定义证明即可
【解析】
试题分析：（1）由
得，
，
整理得：
， 4分
由于对任意的
都成立，所以. 6分
（２） 根据（1）可知
， 8分
下面证明函数
在区间
上是增函数.设
12分
因为
所以
故函数在区间上是增函数. 14分
考点：本小题主要考查函数的对称性的应用和单调性的证明.
点评：由可以得到函数图象关于x=1对称，所以x=1是函数的对称轴，利用这条性质也可以解出a的值；另外，证明函数的单调性时要严格按照单调性的定义进行证明.
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
，且对任意
，有
.
；
在区间（0，1）上为单调函数，求实
数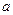
的取值范围.
的零点个数？(提示
)
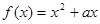，且对任意的实数x都有
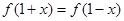成立，求实数a的值；
是减函数，且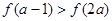
，求a的取值范围。
，且对任意的x、y∈（-1，1）都有
．
．
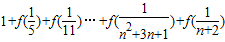的值．
，且对任意的x、y∈（-1，1）都有
．
．
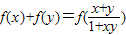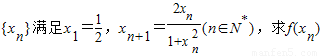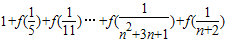的值．