题目内容
20.若$α∈(0,\frac{π}{2})$,方程x2sin2α+y2cos2α=1表示焦点在y轴上的椭圆的条件下长半轴长不小于2的概率是$\frac{2}{3}$.分析 先根据椭圆焦点在y轴上得出α的取值范围,再根据长半轴长不小于2得出α的取值范围,即可求出概率..
解答 解:∵焦点在y轴上
∴sinα>cosα,即sinα>sin($\frac{π}{2}$-α)
∵$α∈(0,\frac{π}{2})$,
∴α>$\frac{π}{2}$-α,即$\frac{π}{2}$>α>$\frac{π}{4}$,
长半轴长不小于2,即$\frac{1}{cosα}$≥2,
∴cosα≤$\frac{1}{2}$,
∵$α∈(0,\frac{π}{2})$,
∴$\frac{π}{2}$>α≥$\frac{π}{3}$,
∴所求概率为$\frac{\frac{π}{2}-\frac{π}{3}}{\frac{π}{2}-\frac{π}{4}}$=$\frac{2}{3}$
故答案为:$\frac{2}{3}$.
点评 本题主要考查了椭圆的标准方程的问题,考查概率的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
11.在圆周上有10个等分,以这些点为顶点,每3个点可以构成一个三角形,如果随机选择了3个点,刚好构成直角三角形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
8.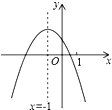 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
①4ac-b2<0;
②4a+c<2b;
③3b+2c<0;
④m(am+b)+b<a(m≠-1),
其中正确结论的个数是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;
②4a+c<2b;
③3b+2c<0;
④m(am+b)+b<a(m≠-1),
其中正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
15.已知:关于x的方程x2+(a2-9)x+a2-5a+6=0的一根小于0,另一根大于2,则a的取值范围是( )
| A. | $a>\sqrt{19}或a<-\sqrt{19}或-\sqrt{3}<a<\sqrt{3}$ | B. | $2<a<\frac{8}{3}$ | ||
| C. | $-1<a<\frac{8}{3}$ | D. | a∈∅ |
10.已知角α的终边经过点(-3,4),则$sin({α+\frac{π}{4}})$的值( )
| A. | $\frac{\sqrt{2}}{5}$ | B. | -$\frac{\sqrt{2}}{5}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | -$\frac{\sqrt{2}}{10}$ |