题目内容
某地兴修水利挖渠,其渠道的横截面为等腰梯形,腰与水平线夹角为60°,要求横截面的周长(包括上底)为定值m,问渠深h为多少时,可使流量最大?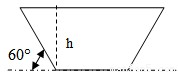
【答案】分析:根据题意,先求腰长与上下底边之和,进而可得面积,要使流量最大,只要求横截面积最大即可.利用配方法可解.
解答:解:设横截面面积为S,有条件知要使流量最大,只要求横截面积最大即可.(1分)
∵腰长为 h,上下底边之和为
h,上下底边之和为 .(3分)
.(3分)
∴S= h(m-
h(m- h),(0<h<
h),(0<h< m)
m)
∴S=- +
+ mh,(0<h<
mh,(0<h< m).(6分)
m).(6分)
∴当h= m时,S取最大值即流量最大.(8分)
m时,S取最大值即流量最大.(8分)
点评:本题以实际问题为载体,考查函数模型的构建,考查函数最值的求解,关键是构建函数模型.
解答:解:设横截面面积为S,有条件知要使流量最大,只要求横截面积最大即可.(1分)
∵腰长为
 h,上下底边之和为
h,上下底边之和为 .(3分)
.(3分)∴S=
 h(m-
h(m- h),(0<h<
h),(0<h< m)
m)∴S=-
 +
+ mh,(0<h<
mh,(0<h< m).(6分)
m).(6分)∴当h=
 m时,S取最大值即流量最大.(8分)
m时,S取最大值即流量最大.(8分)点评:本题以实际问题为载体,考查函数模型的构建,考查函数最值的求解,关键是构建函数模型.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
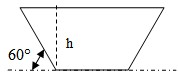 某地兴修水利挖渠,其渠道的横截面为等腰梯形,腰与水平线夹角为60°,要求横截面的周长(包括上底)为定值m,问渠深h为多少时,可使流量最大?
某地兴修水利挖渠,其渠道的横截面为等腰梯形,腰与水平线夹角为60°,要求横截面的周长(包括上底)为定值m,问渠深h为多少时,可使流量最大?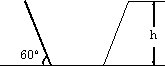
 某地兴修水利挖渠,其渠道的横截面为等腰梯形,腰与水平线夹角为60°,要求横截面的周长(包括上底)为定值m,问渠深h为多少时,可使流量最大?
某地兴修水利挖渠,其渠道的横截面为等腰梯形,腰与水平线夹角为60°,要求横截面的周长(包括上底)为定值m,问渠深h为多少时,可使流量最大?