题目内容
设点P(x,y)(x≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点),点P到定点M((1)求点P的轨迹方程,并说明它表示什么曲线;
(2)若直线l与点P的轨迹相交于A、B两点,且OA⊥OB,点O到直线l的距离为![]() ,求直线l的方程.
,求直线l的方程.
解:(1)依题意得|PM|=d+![]() ,其中d表示点P到y轴的距离,
,其中d表示点P到y轴的距离,
即![]() =|x|+
=|x|+![]() .
.
∵x≥0,∴![]() =x+
=x+![]() .
.
整理得y2=2x.
这就是动点P的轨迹方程,它表示顶点在原点,对称轴为x轴,开口向右的一条抛物线.
(2)a.当直线l的斜率不存在时,由题设可知直线l的方程是x=![]() .
.
联立x=![]() 与y2=2x,可求得点A、B的坐标分别为(
与y2=2x,可求得点A、B的坐标分别为(![]() ,
,![]() )与(
)与(![]() ,-
,-![]() ),此时不满足OA⊥OB,故不合题意.
),此时不满足OA⊥OB,故不合题意.
b.当直线l的斜率存在时,可设直线l的方程为y=kx+b(其中k≠0,b≠0).
将x=![]() 代入y2=2x中,
代入y2=2x中,
并整理得ky2-2y+2b=0. ①
设直线l与抛物线的交点坐标为A(x1,y1)、B(x2,y2),则y1、y2为方程①的两个根,于是y1y2=![]() .又由OA⊥OB可得x1x2+y1y2=0. ②
.又由OA⊥OB可得x1x2+y1y2=0. ②
将x1=![]() 、x2=
、x2=![]() 代入②并整理得y1y2+4=0,∴b+2k=0. ③
代入②并整理得y1y2+4=0,∴b+2k=0. ③
又由点O到直线l的距离为![]() ,得
,得![]() . ④
. ④
联立③④得k=1,b=-2或k=-1,b=2.
故直线l的方程为y=x-2或y=-x+2.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 所表示的平面区域上运动,则z=x+y的最小值是____________.
所表示的平面区域上运动,则z=x+y的最小值是____________.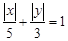 上的点,下列关系正确的是 ( )
上的点,下列关系正确的是 ( ) B.
B. 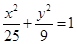
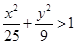 D.
D. 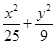 的值与1的大小关系不确定
的值与1的大小关系不确定