题目内容
如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,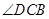 =45
=45 ,O是BC的中点,AO=
,O是BC的中点,AO=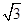 ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2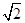 ,
,
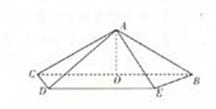
(1)证明:AO⊥平面BCD;(2)求二面角A-CD-B的平面角的正切值.
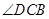 =45
=45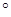 ,O是BC的中点,AO=
,O是BC的中点,AO=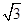 ,且BC=6,AD=AE=2CD=2
,且BC=6,AD=AE=2CD=2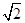 ,
,
(1)证明:AO⊥平面BCD;(2)求二面角A-CD-B的平面角的正切值.
(1)证明详见解析;(2)

试题分析:(1)根据勾股定理证
 ,即
,即 ,再证
,再证 ,直线与平面垂直的判定定理即可得证明;
,直线与平面垂直的判定定理即可得证明;
(2)过O点作
 交CD的延长线于H,根据已知可证
交CD的延长线于H,根据已知可证 二面角A-CD-B的平面角,然后通过解三角形即可求得.
二面角A-CD-B的平面角,然后通过解三角形即可求得.试题解析:(1)易得OC=3,AD=2
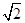 ,连结OD,OE,在∆OCD中,
,连结OD,OE,在∆OCD中,由余弦定理可得OD=
 =
= .
.∵AD=2
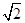 ,∴
,∴ ,∴
,∴ ,
, 同理可证:
 ,又∵
,又∵ ,
, 平面BCD ,
平面BCD ,  平面BCD ,∴AO⊥平面BCD;
平面BCD ,∴AO⊥平面BCD;(2)方法一:过O点作
 交CD的延长线于H,连结AH,因为AO⊥平面BCD,所以
交CD的延长线于H,连结AH,因为AO⊥平面BCD,所以 ,故
,故 为二面角A-CD-B的平面角.
为二面角A-CD-B的平面角.因为OC=3,
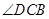 =45
=45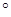 ,所以OH=
,所以OH= ,从而tan
,从而tan =
= .
.
方法二:以O为原点,建立空间直角坐标系O-xyz如图所示.则A(0,0,
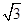 ),C(0,-3,0),D(1,-2,0),
),C(0,-3,0),D(1,-2,0),所以
 =(0,3,
=(0,3,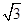 ),
), =(-1,2,
=(-1,2,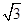 ).
).设
 为平面ACD的一个法向量,则
为平面ACD的一个法向量,则 ,
, 即
 解得
解得 ,令x=1,得
,令x=1,得 .
.由(1)知,
 为平面CDB的一个法向量,所以cos<
为平面CDB的一个法向量,所以cos< >=
>= =
= ,
,由A-CD-B为锐二面角,所以二面角A-CD-B的平面角的正切值为
 .
.
练习册系列答案
相关题目

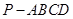 中,底面
中,底面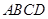 是矩形,
是矩形,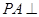 平面
平面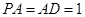 ,
,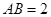 ,
,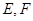 分别是
分别是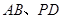 的中点.
的中点.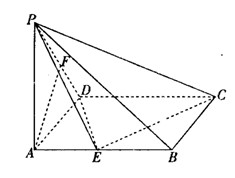
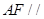 平面
平面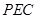 ;
; 的余弦值.
的余弦值.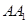 、
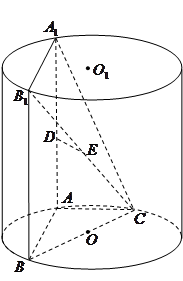
、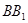 为圆柱
为圆柱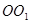 的母线,
的母线,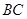 是底面圆
是底面圆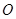 的直径,
的直径,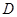 、
、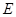 分别是
分别是 的中点,
的中点,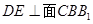 .
.
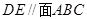 ;
;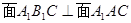 ;
;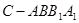 与圆柱
与圆柱 为 正方体的两个顶点,
为 正方体的两个顶点,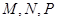 分别为其所在棱的中点,能得出
分别为其所在棱的中点,能得出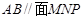 的图形的序号是______.
的图形的序号是______.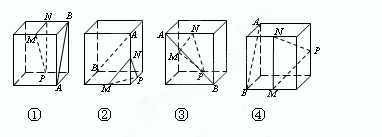
 外有两条直线
外有两条直线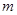 和
和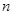 ,如果
,如果 和
和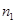 ,给出下列四个命题:①
,给出下列四个命题:① ②
② ③
③
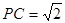 ,求四面体PABC的体积.
,求四面体PABC的体积. 的底面边长为
的底面边长为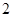 ,高为
,高为 是边
是边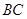 的中点,动点
的中点,动点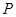 在这个棱锥表面上运动,并且总保持
在这个棱锥表面上运动,并且总保持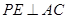 ,则动点
,则动点