题目内容
右图是函数y=sin(ωx+j)(x∈R)在区间[- ,
, ]上的图像,
]上的图像,
为了得到这个函数的图像,只要将y=sinx(x∈R)的图像上所有点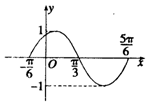
A.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍, 倍,纵坐标不变。 |
B.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变。 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变。 |
C.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变。 倍,纵坐标不变。 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变。 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变。 |
A
解析试题分析:由图象知,T=π,所以 =2,y=sin(2x+j),将(
=2,y=sin(2x+j),将( ,0)代入得:sin(j
,0)代入得:sin(j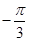 )=0,所以j
)=0,所以j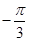 =kπ,
=kπ,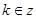 ,取j=
,取j= ,得,y=sin(2x+
,得,y=sin(2x+ ),故只要将y=sinx(x∈R)的图像上所有点向左平移
),故只要将y=sinx(x∈R)的图像上所有点向左平移 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变。故选A。
倍,纵坐标不变。故选A。
考点:本题主要考查三角函数图象变换,三角函数解析式。
点评:基础题,根据图象求函数解析式及三角函数图象的变换均是高考常见题目,本题将二者结合在一起,解得思路明确,应先观察图象,确定“振幅”“周期”,再通过计算求 。
。

练习册系列答案
相关题目
下列函数中,最小正周期为 ,且图象关于直线
,且图象关于直线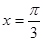 对称的是( )
对称的是( )
A. | B. |
C. | D. |
把函数y=sin 的图象向右平移
的图象向右平移 个单位,再把所得函数图象上各点的横坐标缩短为原来的
个单位,再把所得函数图象上各点的横坐标缩短为原来的 ,所得的函数解析式为( )
,所得的函数解析式为( )
A.y=sin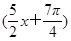 | B.y=sin |
C.y=sin | D.y=sin |
已知函数 的图像如图所示,又
的图像如图所示,又 ,那么
,那么 的值为( )
的值为( )
A. | B. | C. | D. |
将函数 的图像向左平移
的图像向左平移 个单位长度,所得图像的解析式是
个单位长度,所得图像的解析式是
A. | B. |
C.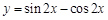 | D. |
 是第四象限角,
是第四象限角, ,则
,则 ( )
( )
A. | B. | C. | D. |
若 ,则
,则 = ( )
= ( )
A. | B. | C.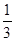 | D. |
点 从
从 出发,沿单位圆逆时针方向运动
出发,沿单位圆逆时针方向运动 弧长到达
弧长到达 点,则
点,则 点的坐标为
点的坐标为
A. | B. | C.  | D. |
设α是第二象限角,P(x,4)为其终边上的一点,且 ,则
,则 =( )
=( )
A. | B. | C. | D. |