题目内容
6．已知点A（1，2），点P（x，y）满足$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-3≤0}\\{x+3y-3≥0}\end{array}\right.$，O为坐标原点，则Z=$\overrightarrow{OA}$•$\overrightarrow{OP}$的最大值为5．分析 根据向量数量积的定义化简目标函数，作出不等式组对应的平面区域，利用目标函数的几何意义进行求解即可．
解答 解：$Z=\overrightarrow{OA}•\overrightarrow{OP}=x+2y$，
作出可行区域如图，
作直线${l_0}：y=-\frac{1}{2}x$，
当l0移到过A（1，2）时，Zmax=1+2×2=5，
故Z=$\overrightarrow{OA}$•$\overrightarrow{OP}$的最大值为5，
故答案为：5．
点评 本题主要考查线性规划的应用，作出不等式组对应的平面区域，利用数形结合是解决本题的关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
1．已知f（x）在R上是减函数，若a=f（log${\;}_{\frac{1}{2}}$8），b=f[（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$]，c=f（2${\;}^{\frac{1}{2}}$）．则（ ）
| A． | a＜b＜c | B． | c＜a＜b | C． | c＜b＜a | D． | a＜c＜b |
11．设△ABC的内角A，B，C的对边分别为a，b，c．若a=2，c=2$\sqrt{3}$，$sinA=\frac{1}{2}$，且b＜c，则B=（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{2π}{3}$ |
18．
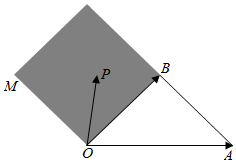如图，OM∥AB，点P在由射线OM，线段OB及AB的延长线围成的阴影区域内（不含边界），且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，则实数对（x，y）可以是（ ）
如图，OM∥AB，点P在由射线OM，线段OB及AB的延长线围成的阴影区域内（不含边界），且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，则实数对（x，y）可以是（ ）| A． | （$\frac{1}{4}$，$\frac{3}{4}$） | B． | （-$\frac{2}{3}$，$\frac{2}{3}$） | C． | （-$\frac{1}{4}$，$\frac{3}{4}$） | D． | （-$\frac{1}{5}$，$\frac{7}{5}$） |
15．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{\sqrt{3}}{4}$，$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$（λ∈R），其中$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为不共线的单位向量，若对符合上述条件的任意向量$\overrightarrow{a}$，$\overrightarrow{b}$恒有|$\overrightarrow{a}$-$\overrightarrow{b}$|≥$\frac{\sqrt{3}}{4}$，则$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$夹角的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5}{6}π$ |