Question

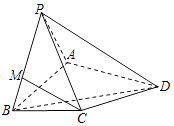
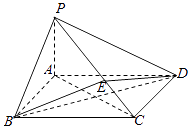
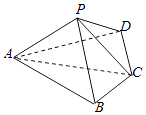
【题目】如图，在三棱锥P﹣ABC中，已知平面PBC⊥平面ABC．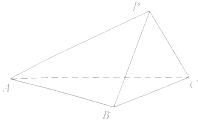

（1）若AB⊥BC，CP⊥PB，求证：CP⊥PA：
（2）若过点A作直线l⊥平面ABC，求证：l∥平面PBC．

Answer 1

【答案】
（1）证明：因为平面PBC⊥平面ABC，平面PBC∩平面ABC=BC，

AB平面ABC，AB⊥BC，所以AB⊥平面PBC．

因为CP平面PBC，所以CP⊥AB．

又因为CP⊥PB，且PB∩AB=B，AB，PB平面PAB，

所以CP⊥平面PAB，

又因为PA平面PAB，所以CP⊥PA．

（2）证明：在平面PBC内过点P作PD⊥BC，垂足为D．

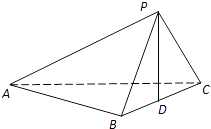
因为平面PBC⊥平面ABC，

又平面PBC∩平面ABC=BC，PD平面PBC，所以PD⊥平面ABC．

又l⊥平面ABC，所以l∥PD．

又l平面PBC，PD平面PBC，所以l∥平面PBC．

【解析】（1）先利用面面垂直的性质定理可证AB⊥平面PBC，进而可证CP⊥AB，再利用线面垂直的判定定理可证CP⊥平面PAB，进而可证CP⊥PA；（2）先过点P作PD⊥BC，垂足为D，再利用面面垂直的性质定理可证PD⊥平面ABC，进而可证l∥PD，从而利用线面平行的判定定理可证l∥平面PBC．