题目内容
【题目】在四棱柱![]() 中,
中,![]() ,
,![]() 且
且![]() ,
,![]() 平面
平面![]() ,
,![]() .
.

(1)证明:![]() .
.
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)根据三角形全等证明AC⊥BD,结合![]() 可得AC⊥平面
可得AC⊥平面![]() ,故而
,故而![]() ;(2)以
;(2)以![]() ,
,![]() 的交点
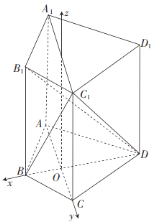
的交点![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,计算平面
,计算平面![]() 的法向量,利用线面角的向量公式求解即可
的法向量,利用线面角的向量公式求解即可
(1)证明:∵AD=CD,∴∠DAC=∠DCA,
又∠BAD=∠BCD,∴∠BAC=∠BCA,∴AB=AC,
∴△ABD≌△CBD,∴∠ADB=∠CDB,
∴△AOD≌△COD,∴∠AOD=∠COD=90°,
∴AC⊥BD,
又因为![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() 所以
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)以![]() ,
,![]() 的交点
的交点![]() 为原点,过O作平行于
为原点,过O作平行于![]() 的直线为z轴,建立如图所示的空间直角坐标系
的直线为z轴,建立如图所示的空间直角坐标系![]() ,由(1)及
,由(1)及![]() ,知
,知![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由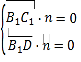 ,得
,得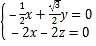 ,
,
所以![]() ,令
,令![]() ,得
,得![]() .
.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则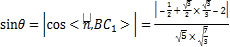
![]() .
.

练习册系列答案
相关题目
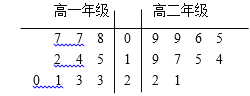
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|