题目内容
16．已知一元二次函数f（x）=ax2+2x+c（a≠0）的图象与y轴交于点（0，1），且满足f（-4）=f（0）．（I）求该二次函数的解析式及函数的零点．
（II）已知函数在（t-1，+∞）上为增函数，求实数t的取值范围．
分析 （I）利用二次函数的图象与y轴交于点（0，1），求出c，利用对称轴求出a，即可得到二次函数的解析式．然后求解零点．
（II）利用函数在（t-1，+∞）上为增函数，对称轴，列出不等式求解即可．
解答 解：（I）因为二次函数为f（x）=ax2+2x+c（a≠0）的图象与y轴交于点（0，1），
故c=1..…．①
又因为函数f（x）满足f（-4）=f（0）故：x=-$\frac{2}{2a}$=-2…..②..…（3分）
由①②得：a=$\frac{1}{2}$，c=1
故二次函数的解析式为：f（x）=$\frac{1}{2}$x2+2x+1 …．（6分）
由f（x）=0，可得函数的零点为：-2$-\sqrt{2}$，-2+$\sqrt{2}$ …（8分）
（II）因为函数在（t-1，+∞）上为增函数，
且函数图象的对称轴为x=-2，
由二次函数的性质可知：t-1≥-2，故t≥-1 …（12分）
点评 本题考查二次函数的解析式的求法，函数的零点以及二次函数的简单性质的应用，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
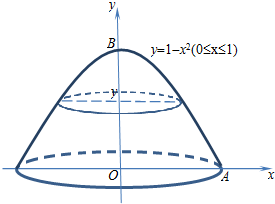在xOy平面上，将抛物线弧y=1-x2（0≤x≤1）、x轴、y轴围成的封闭图形记为D，如图中曲边三角形OAB及内部．记D绕y轴旋转一周而成的几何体为Ω，过点（0，y）（0≤y≤1）作Ω的水平截面，所得截面面积为（1-y）π，试构造一个平放的直三棱柱，利用祖暅原理得出Ω的体积值为$\frac{π}{2}$．
11．将函数f（x）=sin（x+$\frac{π}{6}$）的图象向左平移$\frac{π}{4}$个单位，所得函数g（x）图象的一个对称中心可以是（ ）
| A． | （$\frac{π}{12}$，0） | B． | （-$\frac{π}{12}$，0） | C． | （$\frac{7π}{12}$，0） | D． | （-$\frac{π}{4}$，0） |
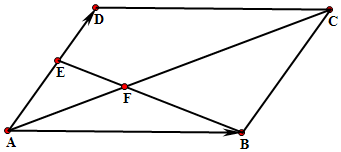如图，平行四边形ABCD中，点E在线段AD上，BE与AC交于点F，设$\overrightarrow{AB}=a，\overrightarrow{AD}=b$．