题目内容
19．函数f（x）=3x-1，若f[g（x）]=2x+3，则g（x）=$\frac{2}{3}x+\frac{4}{3}$．分析 直接利用函数的解析式，求解即可．
解答 解：函数f（x）=3x-1，若f[g（x）]=2x+3，
可得3g（x）-1=2x+3，
解得g（x）=$\frac{2}{3}x+\frac{4}{3}$．
故答案为：$\frac{2}{3}x+\frac{4}{3}$．
点评 本题考查函数的解析式的求法，考查计算能力．
练习册系列答案
相关题目
10．意义运算“*”如下：x*y=$\left\{\begin{array}{l}{x，x≥y}\\{y，x＜y}\end{array}\right.$，若函数f（x）=（1-2x）*（2x-3）+m的图象与x轴有两个交点，则实数m的取值范围是（ ）
| A． | （-1，+∞） | B． | （-1，1） | C． | [-1，+∞） | D． | [-1，1） |
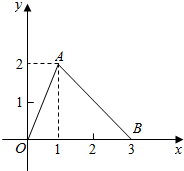函数f（x）的图象是如图所示的折线段OAB，点A的坐标为（1，2），点B的坐标为（3，0），定义函数g（x）=f（x）（1-x）．