题目内容

设a、b、c为正数,且a2+b2=c2.

(1)求证:log2(1+)+log2(1+)=1;

(2)又设log4(1+)=1,log8(a+b-c)=,求a、b、c.

（1）证明：∵左=log2［(1+)·(1+)］

    =log2·

    =log2

    =log2=1=右边，

    ∴等式成立.

（2）解析:由条件得4=1+,       ①

    =a+b-c,                                ②

    由①②得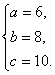


练习册系列答案
相关题目
设a，b，c为正数，利用排序不等式证明a3+b3+c3≥3abc．
设a，b，c为正数，且a+b+4c=1，则
a
+
b
+
2c
的最大值是
10
2
10
2
．
设a，b，c为正数，且a+b+c=1，求证：（a+
1
a
）2+（b+
1
b
）2+（c+
1
c
）2≥
100
3
．
[选做题]
A．（选修4-1：几何证明选讲）
如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交AC于点E，交⊙O于点D，若PE=PA，
∠ABC=60°，PD=1，BD=8，求BC的长．
B．（选修4-2：矩阵与变换）
二阶矩阵M对应的变换将点（1，-1）与（-2，1）分别变换成点（-1，-1）与（0，-2）．
（Ⅰ）求矩阵M的逆矩阵M-1；
（Ⅱ）设直线l在变换M作用下得到了直线m：2x-y=4，求l的方程．
C．（选修4-4：坐标系与参数方程）
在极坐标系中，设圆ρ=3上的点到直线ρ(cosθ+
3
sinθ)=2的距离为d，求d的最大值．
D．（选修4-5：不等式选讲）
设a，b，c为正数且a+b+c=1，求证：(a+
1
a
)2+(b+
1
b
)2+(c+
1
c
)2≥
100
3
．
（理）（1）设x、y是不全为零的实数，试比较2x2+y2与x2+xy的大小；
（2）设a，b，c为正数，且a2+b2+c2=1，求证：
1
a2
+
1
b2
+
1
c2
-
2(a3+b3+c3)
abc
≥3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网