题目内容
设 ,则直线xcosθ+ysinθ+1=0的倾斜角α为
,则直线xcosθ+ysinθ+1=0的倾斜角α为
- A.
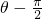
- B.θ
- C.

- D.π-θ
A
分析:直线xcosθ+ysinθ+1=0的斜率等于-cotθ,由tanα=-cotθ=tan(θ- )及 0<θ-
)及 0<θ- <
< 可得 α 的值.
可得 α 的值.
解答:由于直线xcosθ+ysinθ+1=0的斜率等于-cotθ, ,
,
故tanα=-cotθ=tan(θ- ),再由 0<θ-
),再由 0<θ- <
< 可得,α=θ-
可得,α=θ- ,
,
故选A.
点评:本题考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围,得到tanα=-cotθ=tan(θ- ),是解题的关键.
),是解题的关键.
分析:直线xcosθ+ysinθ+1=0的斜率等于-cotθ,由tanα=-cotθ=tan(θ-
 )及 0<θ-
)及 0<θ- <
< 可得 α 的值.
可得 α 的值.解答:由于直线xcosθ+ysinθ+1=0的斜率等于-cotθ,
 ,
,故tanα=-cotθ=tan(θ-
 ),再由 0<θ-
),再由 0<θ- <
< 可得,α=θ-
可得,α=θ- ,
,故选A.
点评:本题考查直线的倾斜角和斜率的关系,以及倾斜角的取值范围,得到tanα=-cotθ=tan(θ-
 ),是解题的关键.
),是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则直线xcosθ+ysinθ+1=0的倾斜角α为( )
,则直线xcosθ+ysinθ+1=0的倾斜角α为( )

 ,则直线xcosθ+ysinθ-1=0的倾斜角是
,则直线xcosθ+ysinθ-1=0的倾斜角是