题目内容
设![]() 两点在抛物线
两点在抛物线![]() 上,l 是AB的垂直平分线,
上,l 是AB的垂直平分线,
(Ⅰ)当且仅当![]() 取何值时,直线 l 经过抛物线的焦点F?证明你的结论;
取何值时,直线 l 经过抛物线的焦点F?证明你的结论;
(Ⅱ)当![]() 时,求直线 l 的方程.
时,求直线 l 的方程.
解:(Ⅰ)F∈l![]() |FA|=|FB|
|FA|=|FB|![]() A、B两点到抛物线的准线的距离相等,
A、B两点到抛物线的准线的距离相等,
∵抛物线的准线是x轴的平行线,y1≥0,y2≥0依题意y1,y2不同时为0,
∴上述条件等份于y1=y2![]()
![]() =
=![]()
![]() (x1+x2)(x1-x2)=0;
(x1+x2)(x1-x2)=0;
∵x1≠x2,
∴上述条件等份于![]() .
.
即当且仅当![]() 时,l经过抛物线的焦点F.
时,l经过抛物线的焦点F.
(Ⅱ)y1=2![]() =2,y2=2
=2,y2=2![]() =18.
=18.
∴过点A、B的直线的斜率为![]() =-4
=-4
∵l与AB垂直,
∴l的斜率为![]() .
.
又线段AB的中点坐标为(![]() ),即(-1,10).
),即(-1,10).
∴l的直线方程为y-10=![]() (x+1).
(x+1).
即所求的方程为x-4y+41=0.

练习册系列答案
相关题目
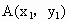 ,
,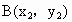 两点在抛物线
两点在抛物线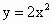 上,l是AB的垂直平分线.
上,l是AB的垂直平分线.
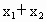 取何值时,直线l经过抛物线的焦点F?证明你的结论;
取何值时,直线l经过抛物线的焦点F?证明你的结论;
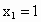 ,
,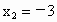 时,求直线l的方程.
时,求直线l的方程.