题目内容
在锐角△ABC中，AC=1，B=2A，则BC的取值范围是________．
（
，
）
分析：根据三角形为锐角三角形，解不等式得
＜A＜
．再由正弦定理，得BC=
，结合余弦函数的单调性加以计算，即可得到BC的取值范围．
解答：∵锐角△ABC中，B=2A，
∴
，解之得＜A＜
∵AC=1，且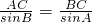
∴BC=
=
=
∵＜A＜，得
＜2cosA＜
∴
＜＜
，得BC=∈（，）
故答案为：（，）
点评：本题给出锐角三角形的一个角是另一角的二倍，求边BC的取值范围，着重考查了三角形内角和定理和利用正、余弦定理解三角形等知识，属于中档题．
，）分析：根据三角形为锐角三角形，解不等式得
＜A＜．再由正弦定理，得BC=，结合余弦函数的单调性加以计算，即可得到BC的取值范围．解答：∵锐角△ABC中，B=2A，
∴
，解之得＜A＜∵AC=1，且
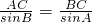
∴BC=
==∵
＜A＜，得＜2cosA＜∴
＜＜，得BC=∈（，）故答案为：（
，）点评：本题给出锐角三角形的一个角是另一角的二倍，求边BC的取值范围，着重考查了三角形内角和定理和利用正、余弦定理解三角形等知识，属于中档题．
练习册系列答案
名师金手指领衔课时系列答案
相关题目