题目内容
13．平面上三个力F1、F2、F3作用于一点且处于平衡位置，|F1|=N，|F2|=$\sqrt{2}$N，F1与F2的夹角为$\frac{π}{4}$，则|F3|=$\sqrt{5}$N．分析 根据题意，画出图形，根据图形即可求出结果．
解答 解：根据题意，画出图形，如图所示；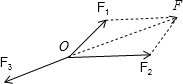
F1与F2的合力是F，
∴$\overrightarrow{OF}$=$\overrightarrow{{OF}_{1}}$+$\overrightarrow{{OF}_{2}}$
∴|$\overrightarrow{OF}$|=|$\overrightarrow{{OF}_{1}}$+$\overrightarrow{{OF}_{2}}$|=$\sqrt{{N}^{2}+2•N•\sqrt{2}Ncos\frac{π}{4}{+（\sqrt{2}N）}^{2}}$=$\sqrt{5}$N
∴|$\overrightarrow{{OF}_{3}}$|=|$\overrightarrow{OF}$|=$\sqrt{5}$N．
故答案为：$\sqrt{5}$．
点评 本题考查了平面向量的应用问题，是基础题目．
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
8．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，左顶点为A，点B（0，b），若线段AF1（不含端点）上存在点P，使得以PF2为直径的圆经过点B，则双曲线C的离心率的取值范围是（ ）
| A． | （1，$\frac{1+\sqrt{5}}{2}$） | B． | （$\frac{1+\sqrt{5}}{2}$，+∞） | C． | （$\sqrt{2}$，$\frac{1+\sqrt{5}}{2}$） | D． | （$\sqrt{2}$，+∞） |
18．若直线y=kx+1与圆x2+（y-1）2=4的两个交点关于直线2x-y+a=0对称，则k，a的值为（ ）
| A． | k=-$\frac{1}{2}$，a=-1 | B． | k=$\frac{1}{2}$，a=-1 | C． | k=$\frac{1}{2}$，a=1 | D． | k=-$\frac{1}{2}$，a=1 |