题目内容
设f（x）=2sin（2x-1）-x，则在下列区间中函数f（x）不存在零点的区间是（ ）A．[-1，0]
B．[0，1]
C．[1，2]
D．[2，3]
【答案】分析：将f（x）=2sin（2x-1）-x的零点转化为函数g（x）=2sin（2x-1）与h（x）=x的交点，在同一坐标系中画出g（x）=2sin（2x-1）与h（x）=x的图象，数形结合对各个区间进行讨论，即可得到答案．
解答：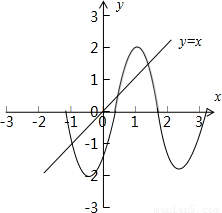
解：在同一坐标系中画出g（x）=2sin（2x-1）与h（x）=x的图象
如下图示：
由图可知g（x）=2sin（2x-1）与h（x）=x的图象在区间[2，3]上无交点，
由图可知函数f（x）=2sin（2x-1）-x在区间[2，3]上没有零点
故选D．
点评：本题主要考查了三角函数图象的平移和函数与方程的相关知识点，突出了对转化思想和数形结合思想的考查，对能力要求较高，属较难题．函数F（x）=f（x）-g（x）有两个零点，即函数f（x）的图象与函数g（x）的图形有两个交点．
解答：
解：在同一坐标系中画出g（x）=2sin（2x-1）与h（x）=x的图象如下图示：
由图可知g（x）=2sin（2x-1）与h（x）=x的图象在区间[2，3]上无交点，
由图可知函数f（x）=2sin（2x-1）-x在区间[2，3]上没有零点
故选D．
点评：本题主要考查了三角函数图象的平移和函数与方程的相关知识点，突出了对转化思想和数形结合思想的考查，对能力要求较高，属较难题．函数F（x）=f（x）-g（x）有两个零点，即函数f（x）的图象与函数g（x）的图形有两个交点．
练习册系列答案
相关题目
设f（x）=cos（x+θ）+
sin（x+φ）是偶函数，其中θ，φ均为锐角，且cosθ=
sinφ，则θ+φ=（ ）
| 2 |
| ||
| 3 |
A、
| ||
| B、π | ||
C、
| ||
D、
|
