题目内容
(10分)动点P到定点D(1,0)的距离与到直线 :
: 的距离相等,动点P形成曲线记作C。
的距离相等,动点P形成曲线记作C。
(1)求动点P的轨迹方程
(2)过点Q(4,1)作曲线C的弦AB,恰被Q平分,求AB所在直线方程.
(1) (2)
(2)
【解析】
试题分析:(1)可根据抛物线的定义得到(2)弦中点问题可利用点差法,设 、
、

 两式相减得
两式相减得 
 ∴
∴ 
试题解析:(1)根据抛物线的定义知:点 的轨迹是焦点为
的轨迹是焦点为 的抛物线,所以轨迹方程是
的抛物线,所以轨迹方程是
(2)设 ,因为
,因为 在抛物线上,所以
在抛物线上,所以 ,(1)-(2)得,
,(1)-(2)得, ,即
,即 ,又因为
,又因为 是
是 的中点,所以
的中点,所以 ,所以直线
,所以直线 的斜率
的斜率 ,所以所以直线
,所以所以直线 的方程为
的方程为 ,即
,即
考点:抛物线的定义,直线与抛物线

练习册系列答案
相关题目
 与直线
与直线 垂直,则
垂直,则
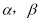 表示不重合的两个平面,
表示不重合的两个平面,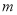 ,
,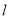 表示不重合的两条直线.若
表示不重合的两条直线.若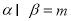 ,
,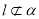 ,
,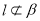 ,则“
,则“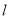 ∥
∥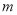 ”是“
”是“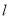 ∥
∥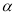 且
且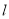 ∥
∥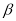 ”的( )
”的( ) 时,
时, 均有意义,则函数
均有意义,则函数 的图像大致是( )
的图像大致是( )
 ,
, ,则
,则 =( )
=( ) B.
B. C.
C. D.
D.
 表示焦点在y轴上的椭圆,则k的取值范围是 ( )
表示焦点在y轴上的椭圆,则k的取值范围是 ( ) 、
、 分别是椭圆
分别是椭圆 的左、右焦点,若Q是该椭圆上的一个动点,则
的左、右焦点,若Q是该椭圆上的一个动点,则 的最大值和最小值分别为( )
的最大值和最小值分别为( ) (x)=
(x)= ,则满足
,则满足 的
的 的取值范围是( )
的取值范围是( )