题目内容
已知cosx+sinx=1,则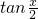 等于
等于
- A.0
- B.1
- C.-1
- D.0或1
D
分析:由题意可得 sin(x+ )=
)= ,∴x=2kπ,或 x=2kπ+
,∴x=2kπ,或 x=2kπ+ ,k∈z,由此求得
,k∈z,由此求得  的值,进而求得
的值,进而求得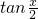 的值.
的值.
解答:∵cosx+sinx=1= sin(x+
sin(x+ ),∴sin(x+
),∴sin(x+ )=
)= ,∴x=2kπ,或 x=2kπ+
,∴x=2kπ,或 x=2kπ+ ,k∈z.
,k∈z.
∴ =kπ,或
=kπ,或  =kπ+
=kπ+ ,k∈z.
,k∈z.
当 =kπ 时,
=kπ 时,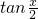 =0; 当 或
=0; 当 或  =kπ+
=kπ+ 时,
时,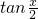 =1,
=1,
故选D.
点评:本题主要考查利用诱导公式进行化简求值,根据三角函数的值求角,体现了分类讨论的数学思想,属于中档题.
分析:由题意可得 sin(x+
 )=
)= ,∴x=2kπ,或 x=2kπ+
,∴x=2kπ,或 x=2kπ+ ,k∈z,由此求得
,k∈z,由此求得  的值,进而求得
的值,进而求得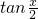 的值.
的值.解答:∵cosx+sinx=1=
 sin(x+
sin(x+ ),∴sin(x+
),∴sin(x+ )=
)= ,∴x=2kπ,或 x=2kπ+
,∴x=2kπ,或 x=2kπ+ ,k∈z.
,k∈z.∴
 =kπ,或
=kπ,或  =kπ+
=kπ+ ,k∈z.
,k∈z.当
 =kπ 时,
=kπ 时,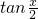 =0; 当 或
=0; 当 或  =kπ+
=kπ+ 时,
时,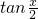 =1,
=1,故选D.
点评:本题主要考查利用诱导公式进行化简求值,根据三角函数的值求角,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目