题目内容
(2012•珠海一模)已知
=(sin(
+x),cos(π-x)),
=(cosx,-sinx),函数f(x)=
•
.
(1)求函数f(x)的最小正周期;
(2)在△ABC中,已知A为锐角,f(A)=1,BC=2,B=
,求AC边的长.
| a |
| π |
| 2 |
| b |
| a |
| b |
(1)求函数f(x)的最小正周期;
(2)在△ABC中,已知A为锐角,f(A)=1,BC=2,B=
| π |
| 3 |
分析:(1)利用向量数量积的坐标运算写出函数f(x),利用倍角公式降幂后化积,则周期可求;
(2)把A代入函数解析式,由f(A)=1结合角A的范围求出角A,然后直接利用正弦定理求AC的长度.
(2)把A代入函数解析式,由f(A)=1结合角A的范围求出角A,然后直接利用正弦定理求AC的长度.
解答:解:(1)由
=(sin(
+x),cos(π-x)),
=(cosx,-sinx),
所以f(x)=
•
=sin(
+x)cosx-sinxcos(π-x)
=cos2x+sinxcosx=
+
sin2x
=
sin(2x+
)+
.
所以T=π;
(2)∵f(A)=cos2A+sinAcosA=1,∴sinAcosA=1-cos2A=sin2A.
∵sinA≠0,∴sinA=cosA.
又A为锐角,∴A=
.
由
=
,∴
=
.
所以AC=
.
所以,AC边的长等于
.
| a |
| π |
| 2 |
| b |
所以f(x)=
| a |
| b |
| π |
| 2 |
=cos2x+sinxcosx=
| 1+cos2x |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
所以T=π;
(2)∵f(A)=cos2A+sinAcosA=1,∴sinAcosA=1-cos2A=sin2A.
∵sinA≠0,∴sinA=cosA.
又A为锐角,∴A=
| π |
| 4 |
由
| AC |
| sinB |
| BC |
| sinA |
| AC | ||
sin
|
| 2 | ||
sin
|
所以AC=
| 6 |
所以,AC边的长等于
| 6 |
点评:本题考查了平面向量数量积的运算,考查了两角和与差的正弦函数,考查了三角函数周期的求法,考查了利用正弦定理求解三角形,解答的关键是熟记有关公式,是中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
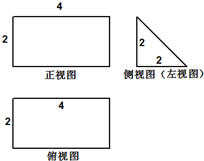 (2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( )
(2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( ) (2012•珠海一模)如图,在△ABC中,已知
(2012•珠海一模)如图,在△ABC中,已知