题目内容
正方体A1C的棱长为a,E、F分别为AB、BC上的点,且(1)设二面角B1-EF-B为α,求tanα.?
(2)试问B1B上是否存在一点G,使得D1G⊥平面B1EF?请证明你的结论.?
(3)求三棱锥D1—B1EF的体积.
解析:(1)如图,连结BD交EF于H,连结B1H.?
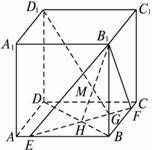
由![]() =3,知EF∥AC,AC⊥平面BB1D1D.?
=3,知EF∥AC,AC⊥平面BB1D1D.?
∴EF⊥平面BB1D1D.?
∴BH⊥EF,B1H⊥EF.?
∠B1HB就是二面角B1-EF-B的平面角.?
∠B1HB=α,B1B=a,BH=![]() ,BD=
,BD=![]() a.?
a.?
∴tanα=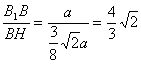 .?
.?
(2)在平面BB1D1D内作D1M⊥B1H,M为垂足,D1M的延长线交B1B于G,则G即为所求.?
∵EF⊥平面BB1D1D,则平面BB1D1D⊥平面B1EF,B1H为平面BB1D1D与平面B1EF的交线,DG在平面BB1D1D内,?
由DG⊥B1H,?
∴DG⊥平面BEF.?
(3)在Rt△B1BH中,B1B=a,BH=![]() BD=
BD=![]() a,?
a,?
∴B1H=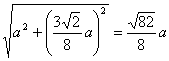 ,?
,?
EF=![]() AC=
AC=![]() .?
.?
∴S△B1EF?=![]() .?
.?
由(2)知D1M就是三棱锥D1—D1EF的高.?
∵B1D1∥BD,?
∴∠D1B1M=∠B1HB=α.?
sinα=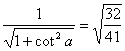 .?
.?
在Rt△D1MB1中,B1D1=![]() a,?
a,?
∴D1M=![]() a.?
a.?
∴VD—B1EF?=![]()
(也可利用B1H•D1M=D1B1•DD1,不必计算B1H和D1M,减少计算量).

练习册系列答案
相关题目
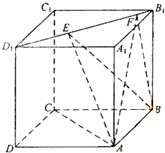 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D上有两个动点E、F,且EF=
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D上有两个动点E、F,且EF=
| ||
| 2 |
| A、AC⊥BE |
| B、A1C⊥平面AEF |
| C、三棱锥A-BEF的体积为定值 |
| D、异面直线AE、BF所成的角为定值 |
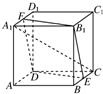 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.
如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.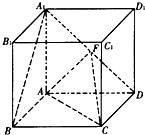 (2009•泰安一模)正方体.ABCD-A1B1C1D1的棱长为l,点F、H分别为为A1D、A1C的中点.
(2009•泰安一模)正方体.ABCD-A1B1C1D1的棱长为l,点F、H分别为为A1D、A1C的中点.