题目内容
若点P(x,y)是曲线C: (θ为参数,0≤θ<π)上的任意一点,则
(θ为参数,0≤θ<π)上的任意一点,则 的取值范围是________.
的取值范围是________.
[- ,0]
,0]
分析:已知曲线C: (θ为参数,0≤θ≤<π),将曲线C先化为一般方程坐标,然后再结合图形计算求
(θ为参数,0≤θ≤<π),将曲线C先化为一般方程坐标,然后再结合图形计算求  的取值范围.
的取值范围.
解答: 解:曲线C的方程可化为(x+2)2+y2=1(y≥0),(3分)
解:曲线C的方程可化为(x+2)2+y2=1(y≥0),(3分)
可见曲线C是以点C(-2,0)为圆心半径为1的上半圆(4分)
设点P(x,y)为曲线C上一动点,
则 =kOP,即O、P两点连线的斜率(6分)
=kOP,即O、P两点连线的斜率(6分)
当P的坐标为 时,
时, 有最小值为
有最小值为  ,
,
当P的坐标为(-1,0)时, 有最大值为0,(9分)
有最大值为0,(9分)
所以 的取值范围是[-
的取值范围是[- ,0](10分)
,0](10分)
故答案为:[- ,0].
,0].
点评:此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
 ,0]
,0]分析:已知曲线C:
 (θ为参数,0≤θ≤<π),将曲线C先化为一般方程坐标,然后再结合图形计算求
(θ为参数,0≤θ≤<π),将曲线C先化为一般方程坐标,然后再结合图形计算求  的取值范围.
的取值范围.解答:
 解:曲线C的方程可化为(x+2)2+y2=1(y≥0),(3分)
解:曲线C的方程可化为(x+2)2+y2=1(y≥0),(3分)可见曲线C是以点C(-2,0)为圆心半径为1的上半圆(4分)
设点P(x,y)为曲线C上一动点,
则
 =kOP,即O、P两点连线的斜率(6分)
=kOP,即O、P两点连线的斜率(6分)当P的坐标为
 时,
时, 有最小值为
有最小值为  ,
,当P的坐标为(-1,0)时,
 有最大值为0,(9分)
有最大值为0,(9分)所以
 的取值范围是[-
的取值范围是[- ,0](10分)
,0](10分)故答案为:[-
 ,0].
,0].点评:此题考查参数方程与普通方程的区别和联系,两者要会互相转化,根据实际情况选择不同的方程进行求解,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数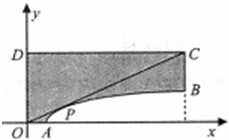 已知图形OAPBCD是由不等式组
已知图形OAPBCD是由不等式组 为坐标原点,
为坐标原点, ,
, 是双曲线
是双曲线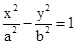 (a>0,b>0)的焦点,若在双曲
(a>0,b>0)的焦点,若在双曲 ,则该双曲线的渐近线方程为(
)
,则该双曲线的渐近线方程为(
) y=0
B.
y=0
B. =0 D.
=0 D. ±y=0
±y=0