题目内容
(本小题满分14分)
在数列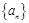 中,
中,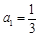 ,且前
,且前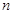 项的算术平均数等于第
项的算术平均数等于第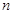 项的
项的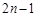 倍(
倍(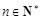 ). (即
). (即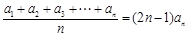
(1)写出此数列的前5项;
(2)归纳猜想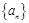 的通项公式,并加以证明.
的通项公式,并加以证明.
在数列
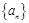 中,
中,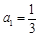 ,且前
,且前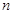 项的算术平均数等于第
项的算术平均数等于第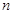 项的
项的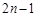 倍(
倍(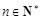 ). (即
). (即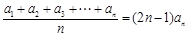
(1)写出此数列的前5项;
(2)归纳猜想
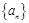 的通项公式,并加以证明.
的通项公式,并加以证明.(1)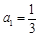 ,
,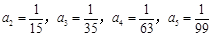 ;
;
(2)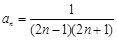 ,证明见解析
,证明见解析
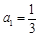 ,
,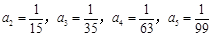 ;
;(2)
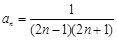 ,证明见解析
,证明见解析(1)此条件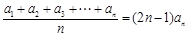 的本质是
的本质是 ,然后令n=1,2,3,4,5,求出前5项即可。
,然后令n=1,2,3,4,5,求出前5项即可。
(2)根据求得的前5项可以归纳出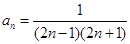 ,由于要证明的结论与n有关,可以考虑采用数学归纳法进行证明:证明要分两个步骤进行:(i)说明n=1时命题成立。(2)先假设n=k时,命题成立;再证明n=k+1时,命题也成立,在证明时要用上n=k时的归纳假设。
,由于要证明的结论与n有关,可以考虑采用数学归纳法进行证明:证明要分两个步骤进行:(i)说明n=1时命题成立。(2)先假设n=k时,命题成立;再证明n=k+1时,命题也成立,在证明时要用上n=k时的归纳假设。
解:(1)由已知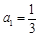 ,
,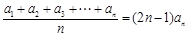 ,分别取
,分别取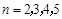 ,
,
得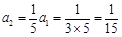 ,
,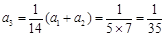 ,
, ,
,
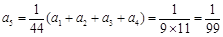 ,所以数列的前5项是:
,所以数列的前5项是: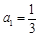 ,
,
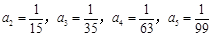 .__4分
.__4分
(2)由(1)中的分析可以猜想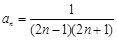 .______6分
.______6分
下面用数学归纳法证明:
①当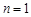 时,公式显然成立.②假设当
时,公式显然成立.②假设当 时成立,即
时成立,即 ,那么由已知,
,那么由已知,
得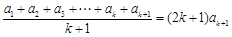 ,
,
即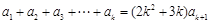 ,所以
,所以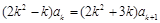 ,
,
即 ,又由归纳假设,得
,又由归纳假设,得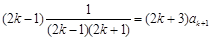 ,
,
所以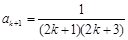 ,即当
,即当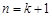 时,公式也成立.
时,公式也成立.
由①和②知,对一切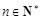 ,都有
,都有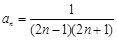 成立. ----------14分
成立. ----------14分
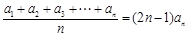 的本质是
的本质是 ,然后令n=1,2,3,4,5,求出前5项即可。
,然后令n=1,2,3,4,5,求出前5项即可。(2)根据求得的前5项可以归纳出
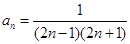 ,由于要证明的结论与n有关,可以考虑采用数学归纳法进行证明:证明要分两个步骤进行:(i)说明n=1时命题成立。(2)先假设n=k时,命题成立;再证明n=k+1时,命题也成立,在证明时要用上n=k时的归纳假设。
,由于要证明的结论与n有关,可以考虑采用数学归纳法进行证明:证明要分两个步骤进行:(i)说明n=1时命题成立。(2)先假设n=k时,命题成立;再证明n=k+1时,命题也成立,在证明时要用上n=k时的归纳假设。解:(1)由已知
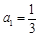 ,
,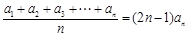 ,分别取
,分别取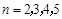 ,
,得
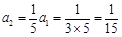 ,
,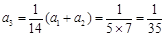 ,
, ,
,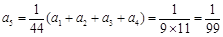 ,所以数列的前5项是:
,所以数列的前5项是: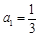 ,
,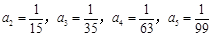 .__4分
.__4分(2)由(1)中的分析可以猜想
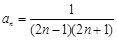 .______6分
.______6分下面用数学归纳法证明:
①当
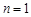 时,公式显然成立.②假设当
时,公式显然成立.②假设当 时成立,即
时成立,即 ,那么由已知,
,那么由已知,得
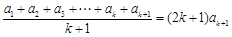 ,
,即
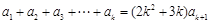 ,所以
,所以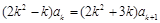 ,
,即
 ,又由归纳假设,得
,又由归纳假设,得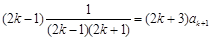 ,
,所以
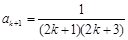 ,即当
,即当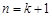 时,公式也成立.
时,公式也成立.由①和②知,对一切
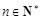 ,都有
,都有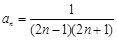 成立. ----------14分
成立. ----------14分
练习册系列答案
相关题目
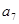 等于()
等于()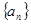 的首项
的首项 ,且满足
,且满足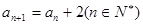 ,则数列
,则数列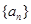 的前n项和
的前n项和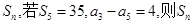 的最大值为( )
的最大值为( )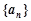 的前4项和为10,且
的前4项和为10,且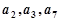 成等比数列.
成等比数列. ;
;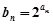 ,求数列
,求数列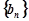 的前
的前 项和
项和 .
.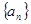 的前三项与数列
的前三项与数列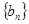 的前三项对应相同,且
的前三项对应相同,且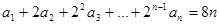 对任意的
对任意的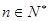 都成立,数列
都成立,数列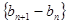 是等差数列
是等差数列
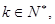 使得
使得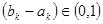 ?请说明理由。
?请说明理由。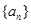 的前
的前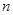 项和为
项和为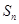 ,公比是正数的等比数列
,公比是正数的等比数列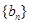 的前
的前 ,已知
,已知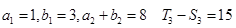
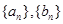 的通项公式。
的通项公式。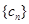 满足
满足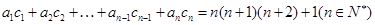 求数列
求数列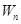 。
。 :
: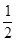 ,
, ,
,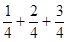 ,
, ,…,那么数列
,…,那么数列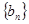 =
=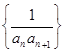 前n项和为( )
前n项和为( )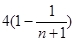
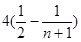

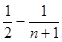
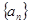 中,
中,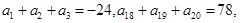 则此数列的前
则此数列的前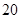 项和 _________.
项和 _________.