题目内容
已知a∈(0,| π |
| 2 |
| 3 |
| 4 |
分析:a∈(0,
),tan(π-a)=-
,由诱导公式求出tana=
,由此可求得角a的终边上一点的坐标是(4,3),求得此点到原点的距离是5,再由三角函数的定义求出sina
| π |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:∵tan(π-a)=-
∴tana=
又a∈(0,
),角是第一象限角,故可取其终边上一点坐标为(4,3),它在原点的距离是5
∴sina=
故答案为
| 3 |
| 4 |
∴tana=
| 3 |
| 4 |
又a∈(0,
| π |
| 2 |
∴sina=
| 3 |
| 5 |
故答案为
| 3 |
| 5 |
点评:本题考查诱导公式的运用,本题中它主要起到了化简转化的作用,解本题关键是熟记诱导公式利用诱导公式进行化简,本题中所涉及到的另一个定义是三角函数的定义,利用定义法求三角函数值是一个基本的方法,题后注意总结作题规律.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
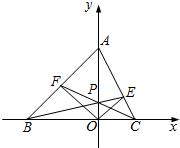 如图,在平面直角坐标系xOy中,已知A(0,2),B(-2,0),C(1,0),P(0,p)(0<p<2),直线BP与AC交于点E,直线CP与AB交于点F,若OE⊥OF,则实数p的值是
如图,在平面直角坐标系xOy中,已知A(0,2),B(-2,0),C(1,0),P(0,p)(0<p<2),直线BP与AC交于点E,直线CP与AB交于点F,若OE⊥OF,则实数p的值是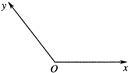 如图,在平面斜坐标系xOy中,∠xOy=135°.斜坐标定义:如果
如图,在平面斜坐标系xOy中,∠xOy=135°.斜坐标定义:如果