题目内容
已知:f(x)=2sin2(ωx+
)-
cos2ωx,两对称轴间的最短距离为
,A为锐角△ABC的内角,若f(A)=
+1.
(Ⅰ)求角A;
(Ⅱ)若△ABC的外接圆半径为
,求△ABC的周长的最大值.
| π |
| 4 |
| 3 |
| π |
| 2 |
| 3 |
(Ⅰ)求角A;
(Ⅱ)若△ABC的外接圆半径为
| 3 |
考点:余弦定理,两角和与差的正弦函数
专题:解三角形
分析:(Ⅰ)利用三角恒等变换化简函数的解析式为 f(x)=1+2sin(2ωx-
),根据周期性求得ω=1,可得f(x)的解析式,再根据f(A)=
+1求得A的值.
(Ⅱ)利用正弦定理求得a=3,又 a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc,bc≤(
)2=
,求得a2≥
,可得b+c的最大值,从而求得周长的最大值.
| π |
| 3 |
| 3 |
(Ⅱ)利用正弦定理求得a=3,又 a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc,bc≤(
| b+c |
| 2 |
| (b+c)2 |
| 4 |
| (b+c)2 |
| 4 |
解答:
解:(Ⅰ)∵f(x)=1-cos(2ωx+
)-
cos(2ωx)=1+sin2ωx-
cos2ωx=1+2sin(2ωx-
),
∵函数的周期T=π=
,∴ω=1,∴f(x)=1+2sin(2x-
),∴f(A)=1+2sin(2A-
)=
+1,
∴sin(2A-
)=
,(0<A<π).
再根据-
<2A-
<
,∴2A-
=
,或2A-
=
,∴A=
,或A=
,根据A为锐角,可得A=
.
(Ⅱ)∵
=2R,a=2
×
=3.
又 a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc,bc≤(
)2=
,∴a2≥(b+c)2-
(b+c)2=
,
∴(b+c)2≤36b+c≤6a+b+c≤9,即周长的最大值为9.
| π |
| 2 |
| 3 |
| 3 |
| π |
| 3 |
∵函数的周期T=π=
| 2π |
| 2ω |
| π |
| 3 |
| π |
| 3 |
| 3 |
∴sin(2A-
| π |
| 3 |
| ||
| 2 |
再根据-
| π |
| 3 |
| π |
| 3 |
| 5π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
(Ⅱ)∵
| a |
| sinA |
| 3 |
| ||
| 2 |
又 a2=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc,bc≤(
| b+c |
| 2 |
| (b+c)2 |
| 4 |
| 3 |
| 4 |
| (b+c)2 |
| 4 |
∴(b+c)2≤36b+c≤6a+b+c≤9,即周长的最大值为9.
点评:本题主要考查三角恒等变换,正弦函数的周期性、正弦定理、基本不等式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
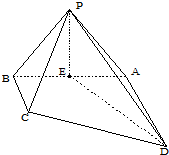 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2=0,BC=
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,∠DAB=90°,AD∥BC,AD⊥侧面PAB,△PAB是等边三角形,DA=AB=2=0,BC=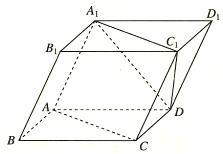 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=∠A1AC=60°,平面AA1CC1⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=∠A1AC=60°,平面AA1CC1⊥平面ABCD.