题目内容
如图,在圆 上任取一点
上任取一点 ,过点
,过点 作
作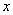 轴的垂线段
轴的垂线段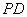 ,
,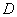 为垂足.设
为垂足.设 为线段
为线段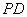 的中点.
的中点.
(Ⅰ)当点 在圆
在圆 上运动时,求点
上运动时,求点 的轨迹
的轨迹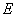 的方程;
的方程;
(Ⅱ)若圆 在点
在点 处的切线与
处的切线与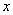 轴交于点
轴交于点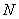 ,试判断直线
,试判断直线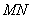 与轨迹
与轨迹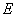 的位置关系.
的位置关系.

解:(Ⅰ)设 ,则
,则 .
. 点
点 在圆
在圆 上,
上, ,
,
即点 的轨迹
的轨迹 的方程为
的方程为 .…………………………………………4分
.…………………………………………4分
(Ⅱ)解法一:(i) 当直线 的斜率不存在时,直线
的斜率不存在时,直线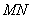 的方程为
的方程为 或
或 .显然与轨迹
.显然与轨迹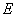 相切;
相切;
(ii)当直线 的斜率存在时,设
的斜率存在时,设 的方程为
的方程为 ,
,
因为直线 与圆
与圆 相切,所以
相切,所以 ,即
,即 .………………7分
.………………7分
又直线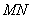 的斜率等于
的斜率等于 ,点
,点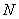 的坐标为
的坐标为 .
.
所以直线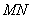 的方程为
的方程为 ,即
,即 . …………………………9分
. …………………………9分
由 得
得 .
.

 .故直线
.故直线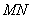 与轨迹
与轨迹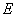 相切.
相切.
综上(i)(ii)知,直线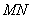 与轨迹
与轨迹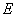 相切. ……………………………………………13分
相切. ……………………………………………13分
解法二 :设 (
( ),则
),则 .……………………………………5分
.……………………………………5分
(i)当 时,直线
时,直线 的方程为
的方程为 或
或 ,此时,直线
,此时,直线 与轨迹
与轨迹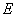 相切;
相切;
(ii)当 时,直线
时,直线 的方程为
的方程为 ,即
,即 .
.
令 ,则
,则 .
. ,又点
,又点 ,
,
所以直线 的方程为
的方程为 ,即
,即 .………………9分
.………………9分
由 得
得 即
即 .
.
 .所以,直线
.所以,直线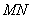 与轨迹
与轨迹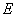 相切.
相切.
综上(i)(ii)知,直线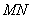 与轨迹
与轨迹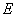 相切.……………………………………………13分
相切.……………………………………………13分

练习册系列答案
相关题目
 有两个零点,则a应满足的充要条件是
有两个零点,则a应满足的充要条件是 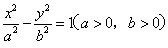 的右焦点为F,若过点F且倾斜角为60°的直线与 双曲线的右支有两个交点,则此双曲线离心率的取值范围是( )
的右焦点为F,若过点F且倾斜角为60°的直线与 双曲线的右支有两个交点,则此双曲线离心率的取值范围是( ) )
)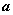 、
、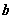 满足
满足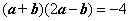 ,且
,且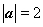 ,
,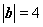 ,
,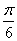 B.
B.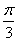 C.
C.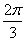 D.
D.
 ,若二次函数
,若二次函数 满足:①
满足:① 与
与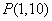 处有公共切线;②
处有公共切线;②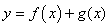 是
是 上的单调函数.则
上的单调函数.则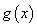 = .
= .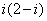 对应的点位于
对应的点位于 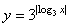 的图像是
的图像是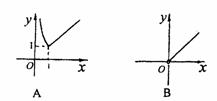
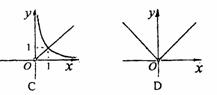
 中,
中,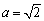 ,
, ,
, ,则A等于
,则A等于 (B)
(B) 
 (D)
(D) 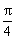 或
或 与直线y=b没有公共点,则b的取值范围是 .
与直线y=b没有公共点,则b的取值范围是 .