题目内容
如图求证:![]() .
.
图
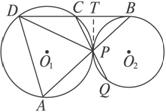
证明:过点P作两圆的公切线PT交BD于T,则∠CPT=∠CDP,
∵BD是⊙O2的切线,
∴∠B=∠BPT.∵∠APD=∠CDP+∠B,∠BPC=∠BPT+∠CPT,
∴∠APD=∠BPC.
又∵∠BCP=∠A,∴△PAD∽△PCB.
∴![]() .
.
∵BC是⊙O2的切线,∴BC2=CP·CQ.
∴![]() .
.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
题目内容
如图求证:![]() .
.

图
证明:过点P作两圆的公切线PT交BD于T,则∠CPT=∠CDP,
∵BD是⊙O2的切线,
∴∠B=∠BPT.∵∠APD=∠CDP+∠B,∠BPC=∠BPT+∠CPT,
∴∠APD=∠BPC.
又∵∠BCP=∠A,∴△PAD∽△PCB.
∴![]() .
.
∵BC是⊙O2的切线,∴BC2=CP·CQ.
∴![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案