Question

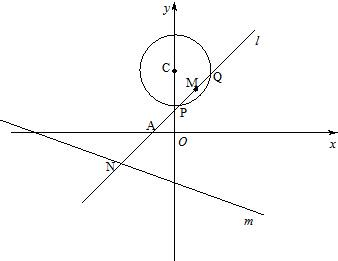如图，已知定圆C：x²+（y-3）²=4，定直线m：x+3y+6=0，过A（-1，0）的一条动直线l与直线相交于N，与圆C相交于P，Q两点，M是PQ中点．
（Ⅰ）当l与m垂直时，求证：l过圆心C；
（Ⅱ）当|PQ|=2

3

时，求直线l的方程；
（Ⅲ）设t=

AM

•

AN

，试问t是否为定值，若为定值，请求出t的值；若不为定值，请说明理由．

Answer 1

分析：（Ⅰ）根据已知，容易写出直线l的方程为y=3（x+1）．将圆心C（0，3）代入方程易知l过圆心C．
（Ⅱ）过A（-1，0）的一条动直线l．应当分为斜率存在和不存在两种情况；当直线l与x轴垂直时，进行验证．当直线与x轴不垂直时，设直线l的方程为y=k（x+1），由于弦长|PQ|=2

3

，利用垂径定理，则圆心C到弦的距离|CM|=1．从而解得斜率K来得出直线l的方程为．
（Ⅲ）同样，当l与x轴垂直时，要对设t=

AM

•

AN

，进行验证．当l的斜率存在时，设直线l的方程为y=k（x+1），代入圆的方程得到一个二次方程．充分利用“两根之和”和“两根之积”去找

AM

．再用两根直线方程联立，去找

AN

．从而确定t=

AM

•

AN

的代数表达式，再讨论t是否为定值．

解答：解：（Ⅰ）由已知km=-

1

3

，故k_l=3，
所以直线l的方程为y=3（x+1）．
将圆心C（0，3）代入方程易知l过圆心C．（3分）
（Ⅱ）当直线l与x轴垂直时，易知x=-1符合题意；（4分）
当直线与x轴不垂直时，设直线l的方程为y=k（x+1），由于|PQ|=2

3

，
所以|CM|=1．由|CM|=

|-k+3|

k2+1

=1，解得k=

4

3

．
故直线l的方程为x=-1或4x-3y+4=0．（8分）
（Ⅲ）当l与x轴垂直时，易得M（-1，3），N(-1，-

5

3

)，
又A（-1，0）则

AM

=(0，3)，

AN

=(0，-

5

3

)，故

AM

•

AN

=-5．即t=-5．（10分）
当l的斜率存在时，设直线l的方程为y=k（x+1），代入圆的方程得（1+k²）x²+（2k²-6k）x+k²-6k+5=0．
则xM=

x1+x2

2

=

-k2+3k

1+k2

，yM=k(xM+1)=

3k2+k

1+k2

，
即M(

-k2+3k

1+k2

，

3k2+k

1+k2

)，

AM

=(

3k+1

1+k2

，

3k2+k

1+k2

)．
又由

y=k(x+1) x+3y+6=0

得N(

-3k-6

1+3k

，

-5k

1+3k

)，
则

AN

=(

-5

1+3k

，

-5k

1+3k

)．
故t=

AM

•

AN

=

-15k-5

(1+k2)(1+3k)

+

-5k(3k2+k)

(1+k2)(1+3k)

=

-5(1+3k)(1+k2)

(1+3k)(1+k2)

=-5．
综上，t的值为定值，且t=-5．（14分）
另解一：连接CA，延长交m于点R，由（Ⅰ）知AR⊥m．又CM⊥l于M，
故△ANR∽△AMC．于是有|AM|•|AN|=|AC|•|AR|．
由|AC|=

10

，|AR|=

5

10

，得|AM|•|AN|=5．
故t=

AM

•

AN

=-|

AM

|•|

AN

|=-5.（14分）
另解二：连接CA并延长交直线m于点B，连接CM，CN，由（Ⅰ）知AC⊥m，又CM⊥l，
所以四点M，C，N，B都在以CN为直径的圆上，
由相交弦定理得t=

AM

•

AN

=-|AM|•|AN|=-|AC|•|AB|=-5．（14分）

点评：（1）用直线方程时，一定要注意分为斜率存在和不存在两种情况．一般是验证特殊，求解一般．
（2）解决直线与圆相交弦相关计算时一般采用垂径定理求解．
（3）涉及到直线和圆、圆锥曲线问题时，常常将直线代入曲线方程得到一个一元二次方程，再充分利用“两根之和”和“两根之积”整体求解．这种方法通常叫做“设而不求”．