题目内容
已知函数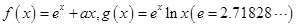 ..
..
(1)设曲线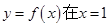 处的切线为
处的切线为 ,点(1,0)到直线l的距离为
,点(1,0)到直线l的距离为 ,求a的值;
,求a的值;
(2)若对于任意实数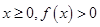 恒成立,试确定
恒成立,试确定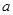 的取值范围;
的取值范围;
(3)当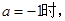 是否存在实数
是否存在实数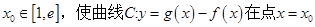 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出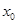 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)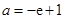 或
或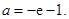 (2)
(2)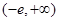 (3)不存在
(3)不存在
解析试题分析:
(1)该问切点横坐标已知,则利用切点在曲线上,带入曲线 即可得到切点的纵坐标,对
即可得到切点的纵坐标,对 进行求导并得到在切点处的导函数值即为切线的斜率,有切线的斜率,切线又过切点,利用直线的点斜式即可求的切线的方程,利用点到直线的距离公式结合条件点
进行求导并得到在切点处的导函数值即为切线的斜率,有切线的斜率,切线又过切点,利用直线的点斜式即可求的切线的方程,利用点到直线的距离公式结合条件点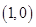 到切线的距离为
到切线的距离为 即可求的参数
即可求的参数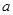 的值.
的值.
(2)该问为恒成立问题可以考虑分离参数法,即把参数a与x进行分离得到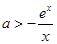 ,则
,则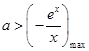 ,再利用函数的导函数研究函数
,再利用函数的导函数研究函数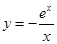 在区间
在区间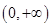 的最大值,即可求的a的取值范围.
的最大值,即可求的a的取值范围.
(3)根据切线的斜率即为曲线C在切点处的导函数值,即该问可以转化为是否存在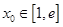 使得
使得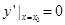 ,令
,令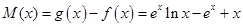 ,则
,则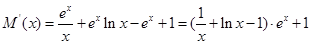 即存在
即存在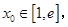 使得
使得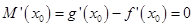 ,对
,对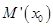 再次求导进行最值求解可得
再次求导进行最值求解可得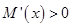 ,所以不存在
,所以不存在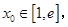 使得
使得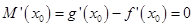 .
.
试题解析:
(1)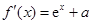 ,
,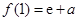 .
.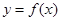 在
在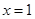 处的切线斜率为
处的切线斜率为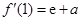 ,
,
∴切线 的方程为
的方程为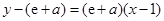 ,即
,即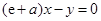 . 2分
. 2分
又点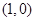 到切线
到切线 的距离为
的距离为 ,所以
,所以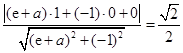 ,
,
解之得,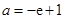 或
或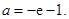 4分
4分
(2)因为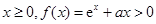 恒成立,
恒成立,
若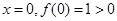 恒成立;
恒成立;
若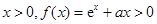 恒成立,即
恒成立,即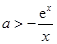 ,在
,在 上恒成立,
上恒成立,
设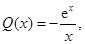 则
则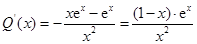
当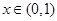 时,
时,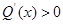 ,则
,则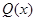 在
在 上单调递增;
上单调递增;
当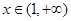 时,
时,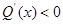 ,则
,则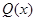 在
在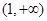 上单调递减;
上单调递减;
所以当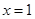 时,
时,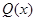 取得最大值,
取得最大值,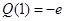 ,
,
所以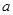 的取值范围为
的取值范围为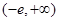 . 9分
. 9分
(3)依题意,曲线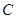 的方程为
的方程为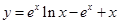 ,令
,令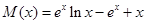
所以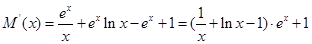 ,
,
设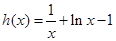 ,则
,则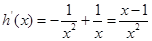 ,当
,当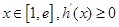 ,
,
故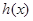 在
在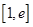 上单调增函数,因此
上单调增函数,因此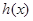 在
在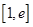 上的最小值为
上的最小值为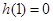
即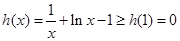
又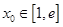 时,
时,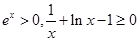
所以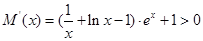
曲线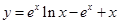 在点
在点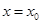

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
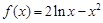
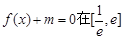 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)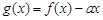 的图象与x轴交于两点
的图象与x轴交于两点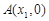 、
、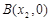 且
且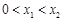 .求证:
.求证: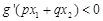 (其中正常数
(其中正常数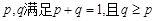 ).
).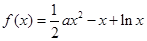 (
(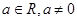 )
) 时,求曲线
时,求曲线 在
在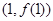 处的切线方程;
处的切线方程; 上函数
上函数 的图象恒在直线
的图象恒在直线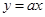 下方,求
下方,求 的取值范围.
的取值范围. (如图所示,其中O为圆心,
(如图所示,其中O为圆心,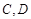 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).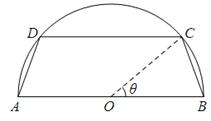
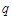 的值,使体积V最大;
的值,使体积V最大;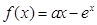
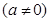 .
.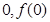 )处的切线方程;
)处的切线方程;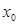 使得
使得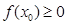 ,求
,求 的取值范围.
的取值范围.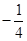 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;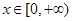 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在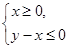 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;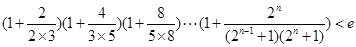 (其中
(其中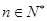 ,e是自然数对数的底数)
,e是自然数对数的底数)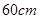 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?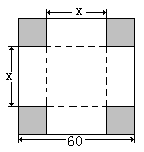
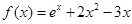 .
. 在区间
在区间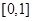 上存在唯一的极值点;
上存在唯一的极值点;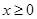 时,若关于
时,若关于 的不等式
的不等式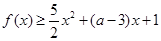 恒成立,试求实数
恒成立,试求实数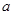 的取值范围.
的取值范围. 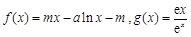 ,其中m,a均为实数.
,其中m,a均为实数.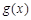 的极值;
的极值;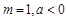 ,若对任意的
,若对任意的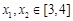
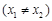 ,
,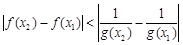 恒成立,求
恒成立,求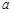 的最小值;
的最小值;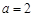 ,若对任意给定的
,若对任意给定的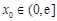 ,在区间
,在区间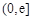 上总存在
上总存在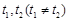 ,使得
,使得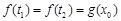 成立,求
成立,求 的取值范围.
的取值范围.