题目内容

【题目】已知直线l：y=x+4，动圆⊙O：x2+y2=r2(1<r<2)，菱形ABCD的一个内角为60°，顶点A、B在直线l上，顶点C、D在⊙O上.当r变化时，求菱形ABCD的面积S的取值范围.

【答案】

【解析】

因为菱形ABCD有一个内角为60°，所以，△ACD或△BCD为等边三角形，不妨设为等边三角形，如图3.

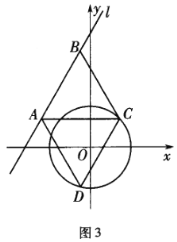
因为圆心O到直线l的距离为2>r，所以，直线l与⊙O相离.

设lCD:y=x-b.

则直线l与CD的距离d=.

又圆心O到直线CD的距离为，故

由

因为1<r<2，所以，3<b2-2b+4<12-2<b<1或1<b<4.

又，

而函数S在区间(-2，1)、区间(1，4)内分别单调递减，故菱形ABCD的面积S的取值范围是.

练习册系列答案
相关题目

【题目】（题文）如图在三棱锥中， 分别为棱的中点，已知，

求证：（1）直线平面；

（2）平面 平面.

【题目】（多选题）下列判断错误的是( )

A.的最小值为2B.{菱形}{矩形}={正方形}

C.方程组的解集为D.如果，那么

【题目】已知函数（a为实常数）.

（1）若，作函数的图象并写出单调减区间；

（2）当时，设在区间上的最小值为，求的表达式；

（3）当时对于函数和函数，若对任意的，总存在使成立，求实数m的值.

【题目】已知f(x)=ln(ax+b)+x2(a≠0).

（1）若曲线y=f(x)在点(1，f（1）)处的切线方程为y=x，求a、b的值；

（2）若f(x)≤x2+x恒成立，求ab的最大值.

【题目】在平面直角坐标系xOy中，过点的圆的圆心C在x轴上，且与过原点倾斜角为30°的直线l相切.

(1)求圆C的标准方程；

(2)求直线被圆C截得的弦长；

(3)点P在直线m：上，过点P作⊙C的切线PM、PN，切点分别为M、N，求经过P、M、N、C四点的圆所过的定点坐标.

【题目】若是素数，证明存在0，1，2，…，的一个排列（，，…，），使得，，，…，.被除的余数各不相同.

【题目】已知函数；

（1）当时，若，求的取值范围；

（2）若定义在上的奇函数满足，且当，，求在上的解析式；

（3）对于（2）中的，若关于的不等式在上恒成立，求实数的取值范围.

【题目】如图，在四棱锥中，已知平面，且四边形为直角梯形，，，.

（1）证明：；

（2）求平面与平面所成锐二面角的余弦值；

（3）点是线段上的动点，当直线与所成的角最小时，求线段的长.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网