题目内容
【题目】若![]() 是素数,证明存在0,1,2,…,
是素数,证明存在0,1,2,…,![]() 的一个排列(
的一个排列(![]() ,
,![]() ,…,
,…,![]() ),使得
),使得![]() ,
,![]() ,
,![]() ,…,
,…,![]() .被
.被![]() 除的余数各不相同.
除的余数各不相同.
【答案】见解析
【解析】
![]() 是素数,由孙子定理,对每个
是素数,由孙子定理,对每个![]() ,存在
,存在![]() ,使得
,使得
![]() 有解
有解![]() .
.
设![]() ,并用
,并用![]() 表示
表示![]() 被
被![]() 除的余数,
除的余数,
则![]() .
.
(1)首先证明![]() ,且
,且![]() 时,
时,![]() .
.
这是因为![]() ,
,
![]() ,
,
![]() .
.
(2)其次证明![]() ,
,![]() .
.
否则,若![]() ,则
,则![]() ,
,![]() ,
,
![]() 时,由于
时,由于![]() ,有
,有 .
.
从而,有

![]()
![]() . (2)
. (2)
从(2),至少有一个![]() ,满足
,满足![]() ,即
,即![]() . (3)
. (3)
如果(3)取等号,则由(2)可知,对于![]() ,
,![]() 不但模长皆为2,而且辐角都应相等.又利用(2)可知
不但模长皆为2,而且辐角都应相等.又利用(2)可知![]() ,则
,则![]() ,这里,
,这里,![]() .再利用(1)可以看到
.再利用(1)可以看到![]() 次多项式
次多项式![]() 当
当![]() 时均为0,从而这多项式恒等于0.那么,
时均为0,从而这多项式恒等于0.那么,
![]() . (4)
. (4)
由于![]() ,
,![]() 从而可以知道
从而可以知道![]() ,
,![]() ,…,
,…,![]() 是一
是一![]() 的
的![]() 次方根.
次方根.
综上所述,![]() .
.
最大值中的最小值达到时,在复平面上,复数![]() ,
,![]() ,…,
,…,![]() 所对应的点是一个单位圆的内接正
所对应的点是一个单位圆的内接正![]() 边形的
边形的![]() 个顶点.
个顶点.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.
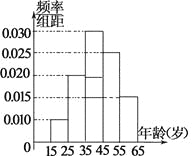
组号 | 分组 | 回答正确 | 回答正确的人数 |
第1组 |
| 5 | 0.5 |
第2组 |
|
| 0.9 |
第3组 |
| 27 |
|
第4组 |
|
| 0.36 |
第5组 |
| 3 |
|
(Ⅰ) 分别求出![]() 的值;
的值;
(Ⅱ) 从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(Ⅲ) 在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.

