Question

【题目】如图是二次函数f（x）=x2﹣bx+a的部分图象，则函数g（x）=ex+f′（x）的零点所在的区间是（ ）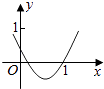
A.（﹣1，0）
B.（0，1）
C.（1，2）
D.（2，3）

Answer 1

【答案】B
【解析】解：由图象可知，0＜f（0）=a＜1①，f（1）=0，即1﹣b+a=0②， 由①②可得1＜b＜2，
g（x）=ex+2x﹣b，且g（0）=1﹣b＜0，g（1）=e+2﹣b＞0，
又g（x）的图象连续不断，所以g（x）在（0，1）上必存在零点，
故选B．
【考点精析】掌握二次函数的性质和基本求导法则是解答本题的根本，需要知道当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减；若两个函数可导，则它们和、差、积、商必可导；若两个函数均不可导，则它们的和、差、积、商不一定不可导．