题目内容
【题目】已知正项数列{an}的前n项和为Sn ， 若{an}和 
都是等差数列，且公差相等．
（1）求数列{an}的通项公式；
（2）令bn= 
，cn=bnbn+1 ， 求数列{cn}的前n项和Tn ．
【答案】
（1）解：∵{an}为等差数列，且Sn为其前n项和，∴ 
，
又∵ 
为等差数列，且与{an}公差相等，
∴ 
，∴ 
，
∴an=a1+（n﹣1）d= 
（2）解：∵ 
Cn=bnbn+1，
∴ 
= 
，
∴Tn=C1+…+Cn= 
【解析】（1）利用等差数列的通项公式与求和公式即可得出．（2）利用裂项求和方法即可得出．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．
练习册系列答案
相关题目
【题目】某电脑公司有6名产品推销员，其工作年限与年推销金额数据如下表：
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限x年 | 3 | 5 | 6 | 7 | 9 |
年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
（1）从编号1﹣5的五位推销员中随机取出两位，求他们年推销金额之和不少于7万元的概率；
（2）求年推销金额y关于工作年限x的线性回归方程 
= 
x+ 
；若第6名产品推销员的工作年限为11年，试估计他的年推销金额． 附：回归直线的斜率和截距的最小二乘法估计公式为： = 
， = 
﹣ 
．
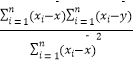