题目内容
已知坐标平面上一点M(x,y)与两个定点M1(26,1),M2(2,1),且

(Ⅰ)求点M的轨迹方程,并说明轨迹是什么图形;
(Ⅱ)记(Ⅰ)中的轨迹为C,过点M(-2,3)的直线l被C所截得的线段的长为8,求直线l的方程.
解:(Ⅰ)由题意,得 =5.
=5.
 ,化简,得x2+y2-2x-2y-23=0………………(3分)
,化简,得x2+y2-2x-2y-23=0………………(3分)
即(x-1)2+(y-1)2=25. ∴点M的轨迹方程是(x-1)2+(y-1)2=25,
轨迹是以(1,1)为圆心,以5为半径的圆.…………………(6分)
(Ⅱ)当直线l的斜率不存在时,l:x=-2,此时所截得的线段的长为2 =8,
=8,
∴l:x=-2符合题意.…………………(8分)
当直线l的斜率存在时,设l的方程为y-3=k(x+2),即kx-y+2k+3=0,
圆心到l的距离d= ,由题意,得(
,由题意,得( )2+42=52,解得k=
)2+42=52,解得k= .
.
∴ 直线l的方程为 x-y+
x-y+ =0,即5x-12y+46=0.
=0,即5x-12y+46=0.
综上,直线l的方程为x=-2,或5x-12y+46=0…………………(12分)

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是( )
| 游戏 | 游戏 | 游戏 |
|
|
|
|
| 取 | 取 | 取 |
| 取出的两个球同色→甲胜 | 取出的球是黑球→甲胜 | 取出的两个球同色→甲胜 |
| 取出的两个球不同色→乙胜 | 取出的球是白球→乙胜 | 取出的两个球不同色→乙胜 |
A. 游戏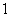 B.游戏
B.游戏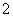 C.游戏
C.游戏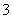 D.游戏
D.游戏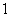 和游戏
和游戏
 =
=  与椭圆
与椭圆 的离心率互为倒数,
的离心率互为倒数, B.
B. C.
C. D.
D. 



 ,则
,则 为:
为:

 为假命题,则
为假命题,则 均为假命题
均为假命题  ,则
,则 ”的逆否命题为:“若
”的逆否命题为:“若 ,则
,则 ”
”  是
是 的必要不充分条件
的必要不充分条件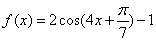 与函数
与函数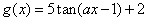 的最小正周期相同,则实数a= .
的最小正周期相同,则实数a= .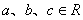 ,若
,若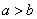 ,则
,则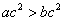 ”,以及它的逆命题、否命题、逆否命题,
”,以及它的逆命题、否命题、逆否命题,