题目内容
已知实数x，y满足
，则s=（x+1）2+（y-1）2的最大值是______．
|
作出不等式对应的平面区域（阴影部分），
∵s=（x+1）2+（y-1）2，
∴s的几何意义是区域内的动点（x，y）到定点P（-1，1）距离平方，
由图象可知当动点位于C时，PC的距离最大．
由
，解得
，
即C（8，-2）．
∴s=（x+1）2+（y-1）2=（8+1）2+（-2-1）2=81+9=90．
故答案为：90．
∵s=（x+1）2+（y-1）2，
∴s的几何意义是区域内的动点（x，y）到定点P（-1，1）距离平方，
由图象可知当动点位于C时，PC的距离最大．
由
|
|
即C（8，-2）．
∴s=（x+1）2+（y-1）2=（8+1）2+（-2-1）2=81+9=90．
故答案为：90．
练习册系列答案
名校课堂系列答案
相关题目
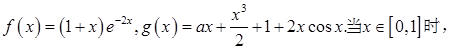
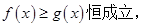
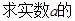取值范围.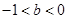
，
，那么下列不等式成立的是（ ）
，1+
＞1，1+
+
+ +
＞
，1+
＞2，1+
＞
， ，由此猜测第n个不等式为 （n∈N*）．
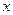是正实数，求证：
；
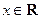，不等式