题目内容
4.已知$\frac{α}{3}$=k•360°+60°(k∈Z),求$\frac{α}{2}$,并指出$\frac{α}{2}$的终边位置.分析 利用$\frac{α}{3}$=k•360°+60°(k∈Z),求$\frac{α}{2}$,分类讨论确定$\frac{α}{2}$的终边位置.
解答 解:∵$\frac{α}{3}$=k•360°+60°(k∈Z),
∴$\frac{α}{2}$=k•540°+90°(k∈Z),
k=2n(n∈Z),$\frac{α}{2}$=3n•360°+90°,终边在y轴的正半轴;
k=2n+1(n∈Z),$\frac{α}{2}$=(3n+1)•360°+270°,终边在y轴的负半轴.
点评 本题考查的知识点是轴线角,熟练掌握各种轴线角所对应的集合形式,并真正理解其几何意义是解答本题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
14.在平面直角坐标系xOy中,点A(2,0),M为不等式组$\left\{\begin{array}{l}{x+y≤1}\\{x+1≥0}\\{x-y≤1}\end{array}\right.$,所表示的区域上一动点,则直线AM斜率的取值范围为( )
| A. | [-3,3] | B. | [-2,2] | C. | [-1,1] | D. | [-$\frac{2}{3}$,$\frac{2}{3}$] |
19.已知命题p;对?x∈R,?m0∈R.使4x+2xm0+1=0.若命题¬p是假命题.则实数m0的取值范围是( )
| A. | .[-2,2] | B. | .[2,+∞) | C. | (-∞,-2] | D. | [-2,+∞) |
14.设x∈R,则“x=±1”是“复数z=(x2-1)+(x+2)i为纯虚数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
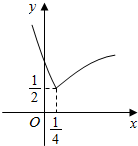 如图所示的函数F(x)的图象是由指数函数f(x)=ax(a>0且a≠1)与幂函数g(x)=xa“拼接“而成的,则下列四个数中最大的是( )
如图所示的函数F(x)的图象是由指数函数f(x)=ax(a>0且a≠1)与幂函数g(x)=xa“拼接“而成的,则下列四个数中最大的是( )