题目内容
圆C：x2+y2+2x-1=0和直线l：3x+4y+8=0交与A，B不同的两点，则三角形△ABC（C为圆心）的面积为（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：直线与圆相交的性质
专题：计算题,直线与圆
分析：把圆C的方程化为标准方程，求得圆心C的坐标和半径，利用点到直线的距离公式求得圆心到直线的距离，根据弦长公式求得弦长AB的值，即可求出△ABC的面积．
解答：
解：圆C的方程x2+y2+2x-1=0即（x+1）2+y2=2，表示以C（-1，0）为圆心，半径等于
的圆．
圆心到直线l：3x+4y+8=0的距离d=
=1
根据弦长公式求得AB=2
=2，
故△ABC的面积为
•2•1=1．
故选：A．
| 2 |
圆心到直线l：3x+4y+8=0的距离d=
| 5 |
| 5 |
根据弦长公式求得AB=2
| 2-1 |
故△ABC的面积为
| 1 |
| 2 |
故选：A．
点评：本题主要考查直线和圆的位置关系，点到直线的距离公式，弦长公式的应用，属于中档题．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
下面四个命题：
①a，b是两个相等的实数，则（a-b）+（a+b）i是纯虚数；
②任何两个复数不能比较大小；
③若z1，z2∈C，且z12+z22=0，则z1=z2=0；
④两个共轭虚数的差为纯虚数．
其中错误的个数有（ ）
①a，b是两个相等的实数，则（a-b）+（a+b）i是纯虚数；
②任何两个复数不能比较大小；
③若z1，z2∈C，且z12+z22=0，则z1=z2=0；
④两个共轭虚数的差为纯虚数．
其中错误的个数有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
甲乙丙三位同学独立的解决同一个问题，已知三位同学能够正确解决这个问题的概率分别为
、
、
，则有人能够解决这个问题的概率为（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=
的定义域为 （ ）
| lg(x+1) |
| x-2 |
| A、（-1，+∞） |
| B、（-∞，2）∪（2，+∞） |
| C、（-1，2）∪（2，+∞） |
| D、（2，+∞） |
平面向量
与
的夹角为60°，
=（1，0），|
|=1，则
•（
-3
）等于（ ）
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
| D、1 |
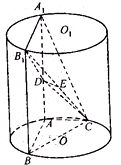如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D、E分别是AA1、CB1的中点，AB=AC．