题目内容
6.集合A={x|x=(2n+1)π,n∈N}与B={x|x=(4n±1)π,n∈N}之间的关系是( )| A. | A?B | B. | B?A | C. | A=B | D. | 不确定 |
分析 先分析两个集合元素的关系.然后利用元素间的关系判断A与B的关系.
解答 解:∵A={x|x=(2n+1)π,n∈N},
∴A集合是所有正奇数的π倍构成的集合
∵B={x|x=(4n±1)π,n∈N},
当n=0时,-π∈B,
∴集合B是由集合A中的所有元素和-π所构成的集合,
∴-π∈B,且-π∉A,
∴A?B,
故选:A
点评 考查整数可分成奇数和偶数,描述法表示集合,以及集合相等的概念.

练习册系列答案
相关题目
16.函数f(x)=a2lnx+x2-3ax在x=1处取到极小值,则实数a的值为( )
| A. | 1 | B. | 2 | C. | 1或$\frac{1}{2}$ | D. | 1或2 |
17.已知点F1(-3,0),F2(3,0),曲线上的动点M满足|MF1|-|MF2|=-4,则该曲线的方程为( )
| A. | $\frac{y^2}{4}$-$\frac{x^2}{5}$=1(y≤-2) | B. | $\frac{y^2}{4}$-$\frac{x^2}{5}$=1 | C. | $\frac{x^2}{4}$-$\frac{y^2}{5}$=1(x≤-2) | D. | $\frac{x^2}{4}$-$\frac{y^2}{5}$=1 |
1.下列结论中,错误的为( )
| A. | 对任意的x∈R,都有2x≥x2成立 | |
| B. | 存在实数x0,使得log${\;}_{\frac{1}{2}}$x0>x0 | |
| C. | 存在常数C,当x>C时,都有2x≥x2成立 | |
| D. | 存在实数x0,使得log${\;}_{\frac{1}{2}}$x0>2${\;}^{{x}_{0}}$ |
11.数字0,1,2,3,4可以组成( )个无重复数字的五位数.
| A. | 96 | B. | 120 | C. | 625 | D. | 1024 |
17.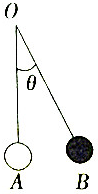 如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )
如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )
 如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )
如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=$\frac{1}{2}$sin(2t+$\frac{π}{2}$),则当t=0时,角θ的大小及单摆频率是( )| A. | $\frac{1}{2}$,$\frac{1}{π}$ | B. | 2,$\frac{1}{π}$ | C. | $\frac{1}{2}$,π | D. | 2,π |
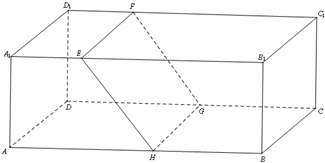 如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.
如图,在长方体ABCD-A1B1C1D1中,AB=16,AA1=8,BC=10,点E,F 分别在A1B1C1D1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形EFGH.